Решение некоторых типовых задач, рассматриваемых в аудитории

13.2.1. Вычислить интеграл , где – внешняя сторона полусферы .

Решение. Дано: , , . Полусфера взаимно-однозначно проектируется на координатную плоскость в круг , заданный неравенством .

Сведем поверхностный интеграл к соответствующему двойному:

. Перейдем к полярным координатам:

. При вычислении учтено, что , поэтому интеграл даже не пришлось находить.

13.2.2. Вычислить поверхностный интеграл , где — часть параболоида , отсеченная плоскостью . Выбрать ту сторону поверхности , для которой .

Решение. Имеем: , . Будем вычислять поток методом проектирования на одну координатную плоскость (а именно, плоскость ) по формуле, аналогичной приведенной в пункте 13.1: Перед интегралом знак минус, потому что вектор образует тупой угол с осью , что указано в условии задачи. Проекцией поверхности на плоскость является круг . Функция , задающая поверхность , равна . Учитывая все это, запишем: . Для вычисления этого двойного интеграла перейдем к полярным координатам:

13.2.3. Вычислить интеграл , где — внешняя сторона полусферы , .

Рис. 13.1

Решение. Векторное поле в этой задаче равно , т. е. , , .

Уравнение поверхности : — нижняя половина сферы радиуса с центром в точке . Эта поверхность однозначно проектируется в круг на плоскости (рис. 13.1). Для подстановки в формулу пункта 13.1 вычислим: . Учтем, что на внешней стороне нижней полусферы нормаль составляет тупой угол с осью , а формула в п. 13.1 записана для случая, когда угол – острый, поэтому поменяем знак: .

Введем полярные координаты с началом в центре круга по формулам , . Тогда

13.2.4. Вычислите поверхностный интеграл , где — часть поверхности гиперболоида , отсекаемая плоскостями и , если нормальный вектор к этой поверхности составляет тупой угол с осью .

Рис. 13.2

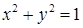Решение. Из вида исходного интеграла получаем компоненты векторного поля: , . Уравнение поверхности . Линии пересечения с указанными в условии плоскостями (подставляем и ) проектируются на плоскость в окружности и соответственно, т. е. проекцией поверхности на плоскость является кольцо (рис. 13.2).

Поскольку выбрана сторона поверхности с , то формула из пункта 13.1 в данном примере берется со знаком минус:

Для вычисления двойного интеграла перейдем к полярным координатам:

13.2.5. Вычислить поток векторного поля через внешнюю сторону полной поверхности пирамиды, образованной плоскостью и координатными плоскостями.

Рис. 13.3

Решение. Найдем сначала потоки векторного поля через грани пирамиды, расположенные в координатных плоскостях. Вычисления будем проводить, следуя определению потока. Так, грань , расположенная в плоскости , является треугольником, ограниченным прямыми , , . Внешней нормалью к этой грани является вектор (см. рис. 13.3), а проекция поля на нормаль равна . Элемент площади . Учитывая, что в этой грани , получим

Перейдем теперь к грани , расположенной в плоскости . Это треугольник, ограниченный прямыми , , . Нормаль , скалярное произведение . Элемент площади . в подынтегральном выражении берется равным , поскольку в этой грани . Итак,

. Аналогично вычисляем поток через грань, расположенную в плоскости : .

Для вычисления потока через грань, лежащую в плоскости , выберем способ проектирования на плоскость (в треугольник ). В формуле имеем , , . Из уравнения плоскости выразим . Подставив все это в формулу для потока, получим .