14.5.1. Вычислить криволинейные интегралы: а)  , где
, где 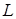 – отрезок прямой
– отрезок прямой  , заключенный между точками
, заключенный между точками  и
и 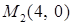 ; б)
; б)  , где
, где 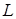 – первая арка циклоиды
– первая арка циклоиды  ,
, 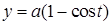 ; в)
; в) 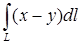 , где
, где 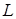 – окружность
– окружность  ; г)
; г)  , где
, где  – четверть окружности
– четверть окружности  ,
, 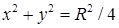 , лежащая в первом октанте.
, лежащая в первом октанте.
14.5.2. Найти координаты центра масс винтовой линии  ,
,  ,
, 
 , считая линию однородной.
, считая линию однородной.
14.5.3. Вычислить площадь части цилиндрической поверхности  , заключенной между плоскостью
, заключенной между плоскостью  и поверхностью
и поверхностью  (
( ).
).
14.5.4. Вычислить криволинейный интеграл  вдоль линии: а)
вдоль линии: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
14.5.5. Вычислить: а)  , где
, где  – отрезок прямой от точки
– отрезок прямой от точки  до точки
до точки  ; б)
; б)  , где
, где  – линия пересечения сферы
– линия пересечения сферы  и цилиндра
и цилиндра  (
( ). Направление обхода линии против часовой стрелки при взгляде из начала координат.
). Направление обхода линии против часовой стрелки при взгляде из начала координат.
14.5.6. Вычислить интеграл  по окружности
по окружности  непосредственно и с помощью формулы Грина.
непосредственно и с помощью формулы Грина.
14.5.7. Проверить, что выражение  является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции  , и найти эту функцию, если: а)
, и найти эту функцию, если: а)  ; б)
; б) 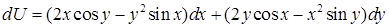 .
.
Ответы. 14.5.1. а)  ; б)
; б) 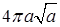 ; в)
; в)  ; г)
; г)  . 14.5.2.
. 14.5.2.  . 14.5.3.
. 14.5.3.  . 14.5.4. а)
. 14.5.4. а)  ; б)
; б) 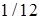 ; в)
; в)  ; г)
; г)  . 14.5.5. а)
. 14.5.5. а)  ; б)
; б)  . 14.5.6.
. 14.5.6.  . 14.5.7. а)
. 14.5.7. а)  ; б)
; б)  .
.
ЧАСТЬ В)
ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ. ФОРМУЛА ГАУССА-ОСТРОГРАДСКОГО
15.1. Дивергенция векторного поля
Дивергенцией векторного поля  называется скалярная функция
называется скалярная функция  .
.
Дивергенция является дифференциальным оператором первого порядка. Она обладает свойством линейности:  , где
, где  — числовая константа.
— числовая константа.
Отметим, что в криволинейных координатах (например, в цилиндрических или сферических) формула для вычисления дивергенции имеет другой вид.
Поток векторного поля через замкнутую поверхность.
 2020-06-29
2020-06-29 122
122








