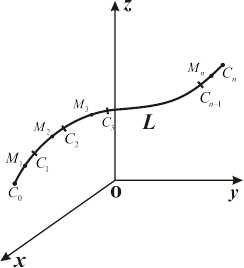
|
| Рис. 14.1 |
Криволинейный интеграл первого рода — это интеграл от некоторой функции (скалярного поля) 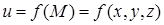 по длине дуги линии
по длине дуги линии 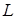 . Именно, разобьем кривую
. Именно, разобьем кривую 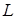 точками
точками 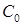 ,
, 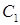 , …,
, …, 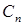 на
на 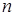 элементарных дуг, в каждой из которых выберем точку
элементарных дуг, в каждой из которых выберем точку 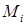 (
(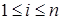 ), как показано на рис. 14.1. Пусть длина элементарной дуги равна
), как показано на рис. 14.1. Пусть длина элементарной дуги равна 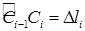 . Составим интегральную сумму
. Составим интегральную сумму 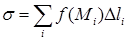 . Назовем характеристикой (мелкостью) разбиения
. Назовем характеристикой (мелкостью) разбиения 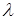 наибольшую длину элементарной дуги:
наибольшую длину элементарной дуги: 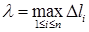 . Тогда предел интегральных сумм
. Тогда предел интегральных сумм 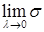 , не зависящий от способа разбиения и выбора точек, называется криволинейным интегралом первого рода
, не зависящий от способа разбиения и выбора точек, называется криволинейным интегралом первого рода 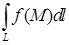 . Для вычисления криволинейного интеграла по кривой, расположенной в плоскости
. Для вычисления криволинейного интеграла по кривой, расположенной в плоскости 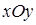 , следует использовать формулу дифференциала длины дуги
, следует использовать формулу дифференциала длины дуги 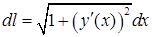 , где
, где 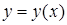 – уравнение кривой
– уравнение кривой 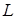 (см. п. 3.2). Тогда
(см. п. 3.2). Тогда
 .
.
Здесь 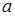 и
и 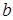 – значения координаты
– значения координаты 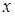 начальной и конечной точки кривой соответственно (
начальной и конечной точки кривой соответственно (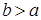 ). В полярных координатах криволинейный интеграл первого рода по плоской кривой вычисляется по формуле
). В полярных координатах криволинейный интеграл первого рода по плоской кривой вычисляется по формуле
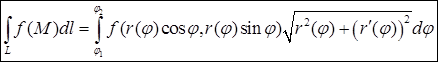 .
.
В общем случае кривую 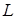 удобно задать параметрически:
удобно задать параметрически: 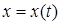 ,
,  ,
, 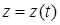 ,
, 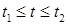 , тогда
, тогда
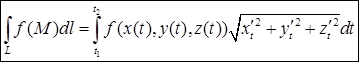 .
.
Если 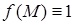 , то криволинейный интеграл первого рода численно равен длине дуги кривой
, то криволинейный интеграл первого рода численно равен длине дуги кривой  между начальной и конечной точками. При произвольной подынтегральной функции он равен массе кривой
между начальной и конечной точками. При произвольной подынтегральной функции он равен массе кривой 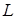 с переменной линейной плотностью
с переменной линейной плотностью 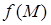 . Среднее арифметическое значение функции
. Среднее арифметическое значение функции 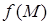 на линии
на линии 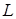 равно
равно 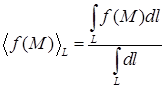 .
.
 2020-06-29
2020-06-29 83
83








