2020-06-29
79
|
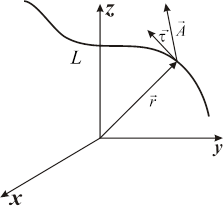
| Рис. 14.2 |
Криволинейный интеграл второго рода иначе называют криволинейным интегралом по координатам. Пусть задано векторное поле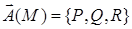 
(см. п. 13.1) и кривая 
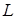. Для вычисления криволинейного интеграла второго рода необходимо выбрать направление обхода кривой, т. е. в каждой точке линии 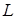задать единичный касательный вектор 
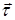, меняющийся от точки к точке непрерывным образом (рис. 14.2). Тогда криволинейный интеграл первого рода от проекции векторного поля 
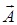на вектор 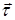и называется криволинейным интегралом второго рода. Проекция 
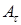равна скалярному произведению 
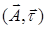, т. к. 
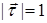, а интеграл задается формулой 
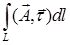. Легко видеть, что 
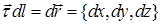, где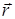 
– радиус-вектор текущей точки линии 
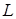. Тогда 
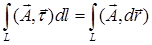. Из этой векторной записи легко усмотреть физический смысл криволинейного интеграла второго рода: это работа силы 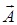при перемещении вдоль кривой 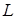. Перейдем от векторной записи к координатной, вычисляя скалярное произведение под интегралом: 
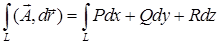. Для вычисления интеграла линию 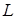зададим параметрически. Тогда
.
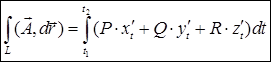Обращаем внимание, что вместо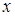 
, 
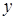и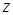 
в аргументах функци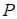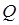й 
, 
и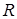 
следует подставить их выражения через параметр 
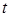, поэтому последняя формула сводит вычисление криволинейного интеграла второго рода к определенному интегралу. Заметим, что здесь, в отличие от интеграла первого рода, не обязательно 
. Нижний и верхний пределы интегрирования определяются значениями параметра в начальной и конечной точке контура 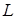при выбранном (заданном) направлении обхода.
В плоском случае поле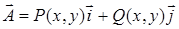 
, тогда
.
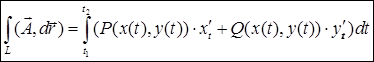Если кривая 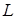задана явно (
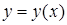), применяется формула
.
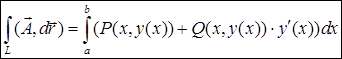Формула Грина
Пусть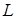 
— замкнутый контур, расположенный в плоскости 
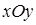. Криволинейный интеграл второго рода 
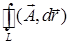можно свести к двойному по формуле Грина:
.
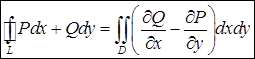Здесь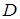 
– область, ограниченная контуром 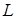, который обходится в положительном направлении, т. е. против часовой стрелки. При изменении направления обхода контура интеграл 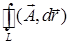меняет знак.
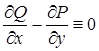— условие независимости интеграла 
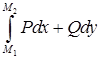от пути, соединяющего точк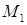и 
и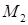 
. При этом выражение 
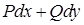является полным дифференциалом некоторой функции двух переменных 
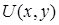, а сама функция может быть найдена по формуле 
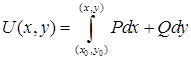, где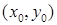 
— произвольная точка, в которой функци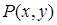и 
и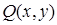 
определены.
