Решение некоторых типовых задач, рассматриваемых в аудитории

14.4.1. Вычислите интеграл по дуге параболы между точками и .

Решение. Вычислим дифференциал длины дуги . Здесь , поэтому . Криволинейный интеграл сводится к определенному интегралу: .

14.4.2. Вычислить с помощью криволинейного интеграла площадь части цилиндрической поверхности , ограниченной снизу плоскостью , а сверху поверхностью .

Рис. 14.3

Решение. Если направляющей цилиндрической поверхности является кривая , лежащая в плоскости , а образующие параллельны оси , причем для каждой образующей точка лежит на кривой , а точка – на поверхности , ограничивающей цилиндрическую поверхность сверху (рис. 14.3), то площадь участка цилиндрической поверхности можно вычислить с помощью криволинейного интеграла: . В этом заключается геометрический смысл криволинейного интеграла первого рода.

В нашем примере для вычисления интеграла удобно задать кривую 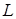(окружность ) параметрически: , . Дифференциал длины дуги равен .

Тогда .

14.4.3. Вычислить криволинейный интеграл , где 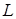— первый виток винтовой линии , , .

Решение. Вычислим дифференциал длины дуги винтовой линии:

. Подынтегральная функция на кривой равна . Первому витку винтовой линии отвечает изменение параметра от до , тогда

14.4.4. Вычислить интеграл по части линии пересечения поверхностей , , лежащей в первом октанте.

Решение. Первая поверхность — сфера радиуса с центром в начале координат, вторая — плоскость, проходящая через центр сферы. Пересечением этих поверхностей является окружность. Зададим ее параметрически. Подставив в уравнение сферы, получим . Этому уравнению тождественно удовлетворяет подстановка , . Следовательно, параметрическими уравнениями линии будут , , . Участку в первом октанте отвечает изменение параметра от до . Вычислим дифференциал длины дуги . Отсюда

14.4.5. Вычислить криволинейный интеграл , где 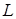— правый лепесток лемнискаты .

Решение. Уравнение лемнискаты удобнее записать в полярных координатах: . Для правого лепестка . Для лемнискаты . Тогда искомый интеграл запишем в виде:

14.4.6. Вычислить интеграл вдоль линий: а) ; б) ; в) .

Решение. а) .

б) .

в) Здесь удобнее перейти к интегрированию по переменной , тогда

, , .

Очевидно, криволинейный интеграл между двумя точками зависит от дуги, соединяющей эти точки.

14.4.7. Найти криволинейный интеграл второго рода вдоль линии пересечения поверхностей и .

Решение. Зададим линию параметрически. Именно, пусть , тогда и . Параметр при этом изменяется от до .

Вычислим дифференциалы переменных: , , . Криволинейный интеграл равен .

14.4.8. Найти работу силы вдоль кривой ориентированной против часовой стрелки со стороны оси .

Решение. Зададим контур параметрически: , . Легко проверить, что уравнения системы при этом превращаются в тождественные равенства. Обходу контура против часовой стрелки, если смотреть со стороны оси абсцисс, отвечает изменение параметра от до . Работа силы задается интегралом

14.4.9. Вычислить интеграл , если — контур треугольника с вершинами , , .

Решение. Преобразуем криволинейный интеграл второго рода по замкнутому контуру в двойной по формуле Грина (см. пункт 14.3).

Найдем .

Тогда

Рис. 14.4

Здесь контур треугольника обходится против часовой стрелки, как показано на рис. 14.4, а область — треугольник . Непосредственное вычисление криволинейного интеграла дает тот же результат, но требует большего количества выкладок.

14.4.10. Проверить, что выражение является полным дифференциалом некоторой функции , и найти эту функцию.

Решение. , ; , . Очевидно, что , т. е. условие полного дифференциала выполнено.

Найдем функцию по формуле , при этом воспользуемся независимостью криволинейного интеграла от пути интегрирования и соединим точки и ломаной линией, состоящей из двух звеньев: и , соединяющих точки , и . Итак, .

На отрезке и , отсюда . На отрезке координата не меняется (), а ордината изменяется от до , поэтому . Складывая вычисленные интегралы, получим . Учитывая, что в качестве начальной точки можно было выбрать не , а любую другую точку, запишем общий вид искомой функции: , где – произвольная постоянная.