2020-06-29
87
15.3.1. Найти дивергенцию векторного поля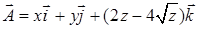 
.
Решение. Координаты векторного поля: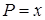 
, 
, 
. По формуле п. 15.1 находим 
.
Итак, 
.
15.3.2. Вычислить поток векторного поля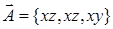 
через внешнюю сторону замкнутой поверхности, образованной параболоидом вращения 
и плоскостью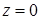 
.
Решение. Найдем 
. Воспользуемся формулой Гаусса-Остроградского: 
. Для вычисления тройного интеграла заметим, что пересечением параболоида и плоскости является окружность 
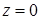, лежащая в плоскости , и для любой точки круга 
координата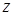 
меняется от 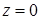(на плоскости) до 
(на параболоиде):
.
15.3.3. Вычислить поток вектора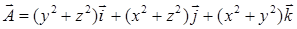 
через внешнюю сторону полусферы 
, 
.
|
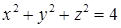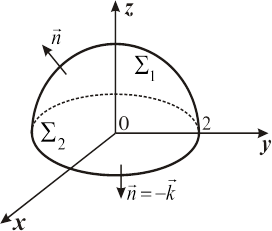
| Рис. 15.2 |
Решение. Полусфера не является замкнутой поверхностью, но дивергенция данного векторного поля равна нулю. Согласно формуле Гаусса-Остроградского, поток вектора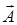 
через любую замкнутую поверхность в этом случае тоже равен нулю. Поэтому, для вычисления потока 
через полусферу 
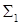, замкнем эту поверхность кругом 
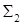(рис. 15.2). Тогда полный поток по формуле Гаусса-Остроградского равен 
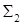. Поток через круг вычислим непосредственно. Внешней нормалью к кругу 
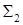является вектор 
, поэтому 
.
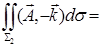
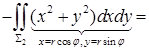
15.3.4. Вычислить поток векторного поля 
через полную поверхность пирамиды с вершинами в точках 
, 
, 
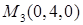и 
.
Решение. Найдем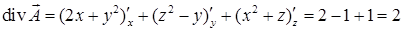 
, тогда по формуле Гаусса-Остроградского полный поток 
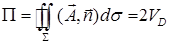, где 
– объем пирамиды. Но 
, отсюда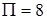 
.
15.3.5. Вычислить поток вектора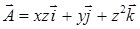 
через внешнюю сторону цилиндрической поверхности 
, 
.
Решение. Замкнем поверхность, добавив к ней два круга: нижнее основание цилиндра 
, 
(поверхность 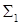) и верхнее основание 
, 
(поверхность 
), как показано на рис. 15.3.
|
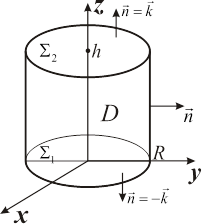
| Рис. 15.3 |
Внешней нормалью к поверхности 
является вектор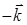 
, откуда 
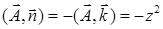, но на поверхности 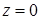, значит, 
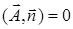и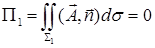 
. Внешней нормалью к является вектор 
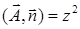, но на координата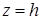 
, откуда
. Теперь воспользуемся формулой Гаусса-Остроградского для вычисления искомого потока 
через цилиндрическую (боковую) поверхность. Найдем 
, тогда 
. Здесь тройной интеграл по области 
, ограниченной цилиндрической поверхностью и кругам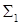и и мы свели к повторному, но 
, а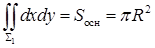 
, поэтому
.
15.3.6. Вычислить поток векторного поля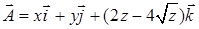 
через внешнюю сторону границы области, ограниченной поверхностями 
и 
.
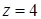Решение. Дивергенция этого поля вычислена в примере 15.3.1. Верхней границей области является плоскость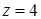 
, нижней – поверхность 
, уравнение которой перепишем в виде 
. Это пределы интегрирования по переменной 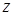. Проекцией области на плоскость 
является фигура 
, ограниченная линией пересечения указанных в условии поверхностей. Подставив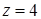 
в уравнение 
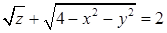, найдем, что 
. Следовательно, 
это круг радиуса 
. По формуле Гаусса-Остроградского поток поля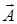 
равен 
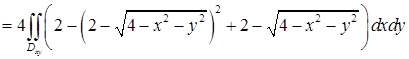. Перейдем к полярным координатам: 
Задачи для самостоятельного решения
