2020-06-29
79
Пусть задано векторное поле 
, где 
, 
и 
— непрерывно дифференцируемые функции точки 
. Поток вектора 
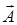через замкнутую кусочно-гладкую поверхность 
равен тройному интегралу от дивергенции этого вектора по области 
, ограниченной поверхностью :
(формула Гаусса-Остроградского). Здесь 
– элемент объема, в декартовых координатах равный 
.
При этом для вычисления потока выбирают внешнюю сторону поверхности 
, т. е. нормаль 
направлена вовне, а не вовнутрь поверхности (рис 15.1).
|
| Рис. 15.1 |
При изменении направления нормали на противоположное величина потока меняет знак. В координатной записи формула Гаусса-Остроградского имеет вид:
.
