Тема 4. Аналітична геометрія на площині. Пряма лінія на площині

1 2 3 4 5 6 7

1. Основні задачі аналітичної геометрії.

2. Різновиди рівнянь прямої лінії на площині.

2.1. рівняння прямої з кутовим коефіцієнтом: y = kx + b; рівняння вертикальної прямої: х = а

2.2. рівняння прямої, яка проходить через дану точку в заданому напрямі:

у – у₁ = kx – kx₁; y – y₁ = k (x – x₁)

2.3. рівняння прямої через 2 дані точки:

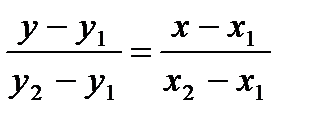
2.4. загальне рівняння прямої:

Аx + By + C = 0

3. Взаємне розміщення двох прямих на площині

3.1. точка перетину прямих:

3.2. кут між прямими: tgα =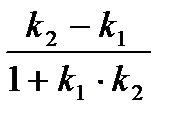

3.3. умова паралельності прямих:

k₂ = k₁

3.4. умова перпендикулярності прямих:

k₁∙k₂ = -1

4. Множина розв’язків системи лінійних нерівностей

5. Задачі на пряму лінію

1. Лінія – це геометричне місце точок, координати яких задовольняють певним властивостям, тобто рівнянню:

F (x; y) = 0 (4.1)

х² + у² = 0 – не є лінією

х² + у² = 1 – не є лінією

Основні задачі:

1) За заданими властивостями лінії скласти її рівняння;

2) Задано рівняння ліній, вивчити її властивості і побудувати графік;

2.1. Дано, що пряма лінія утворює з віссю ОХ кут γ і на осі ОY відтинає відрізок ОВ. Скласти її рівняння.

у М

х х

tg γ =

tg γ = k – кутовий коефіцієнт прямої

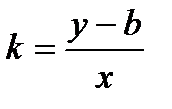, y-b = kx

y = kx + b (4.2)

х, у – координати довільної точки, b – відрізок на осі OY

у = -2х + 3

у′ = k, (kx)′ = k1

Для вертикальної прямої γ = 90°, а tg 90° не існує, тобто не існує кутового коефіцієнту і вона не описується рівнянням (4.2)

х = а (4.2*)

Рівняння (4.2), (4.2*) в сукупності задають все можливі прямі на площині:

ОХ: у = 0

OY: х = 0

γ = 0, то у = b – горизонтальна лінія

2.2. А (х;у), k – дано

Скласти рівняння

т. А → (2.1): у₁= kx₁ + b

b = y₁ – kx₁→ (2.1)

y₂ = kx + y₁ – kx₁

y₂ – y₁ = kx – kx₁, y₂ – y₁ = k (x – x₁)

2.3. A (x₁;y₁), B (x₂;y₂)

B → (2.2): y₂ – y₁ = k (x₂ – x₁)

k = (6.2) → (2.2): y – y₁ = (x – x₁),

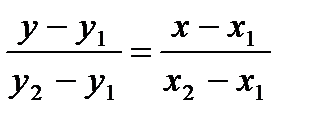
Задача 1.

Скласти рівняння прямої, яка проходить через т. А (-3;2) і утворює з віссю ОХ γ = 45°

Розв’язання:

y – y₁ = k (x – x₁)

k = tg 45° = 1

y – 2 = 1(x+3)

y = x + 3 + 2

y = x + 5

Задача 2.

Скласти рівняння прямої, яка проходить через т. А (2;-1), В (3;2)

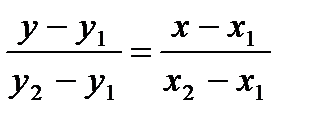
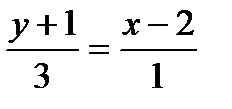
у + 1 = 3 (х – 2)

у + 1 = 3х – 6, у = 3х – 7

Задача 3.

Побудувати прямі:

1) у = -3х + 2

2) 3у – 2х + 6 = 0

3) у = 2х

4) х – 4 = 0

5) 2у – 3 = 0

2.4. Теорема 1

Рівняння першого порядку з двома змінними задає пряму лінію на площині

Аx + By + C = 0 (2.1)

Доведення:

By = -Ax – C

1) B ≠ 0, тоді у =

y = kx + b

2) B = 0, Ax + C = 0

x = Q

Теорема 2 (обернена)

Пряма лінія задається рівнянням першого порядку.

Доведення:

y = kx + b, x = a

3.1. Взаємне розміщення на площині

3.2. Кут між прямими γ = γ + α

у α = γ – γ

tg α = (tg (γ – γ) =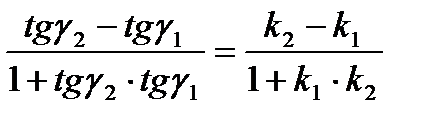

tg α = (4.4)

0 х

Задача 4.

Знайти кут між прямими і точку перетину прямих:

1) 3х – у + 5 = 0

2) –х + 2у + 1 = 0

3х – у = -5

-х + 2у = -1

∆у =│^{3 -1}│= 6 – 1 = 5

^{-1 2}

∆х =│^{-5 -1}│= -10 – 1 = -11

^{-1 2}

∆і = │^{3 -5}│= -3 – 5 = -8

^{-1 -1}

х = , у =

у = 3х + 5 l₁ = 3

y = ½x – ½ l₂ = ½

tg α = =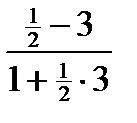

3.3. l₁║l₂; α = 0°, tg 0° = 0 = k₂ – k₁ = 0 k₂ = k₁- умова паралельності прямих.

3.4. l₂║l₁; α = 90°, tg 90° = Э (3.2): = Э 1 + k₂∙k₁ = 0 – умова перпендикулярності прямих.

Задача 5.

Скласти рівняння прямої, яка проходить через точку А (-3;2)

1)║ 2х – 3у + 5 = 0

2) 2х – 3у + 5 = 0

y – y₁ = k (x – x₁)

k₂ = k₁

3y = 2x + 5

y = 2) y – y₁ = k (x – x₁)

k₁ = ; k₂ = k₁=

y – 2 = (x + 3) y – 2 =

y = + 2 + 2 y =

y = y =

Зауваження:

Середина відрізка знаходиться за формулами:

х = х1 + х2 ; у = у1 + у2 .

2 2

4. Множина розв’язків системи

Якщо розв’язками рівняння Ах + Ву + С = 0 є точки, які лежать на прямій, то розв’язками нерівності Ах + Ву + С > 0 буде півплощина обмежена цією прямою. Розв’язками системи нерівностей є спільна частина всіх півплощин, яка називається множиною розв’язків системи нерівностей.

Ця множина може бути відкрита, а може бути обмежена.