План
1. Поняття n- вимірного вектора і лінійного вимірного простору.
2. Базис і розмірність лінійного n- векторного простору.
3. Перехід від одного базиса до іншого в лінійному.
1. n- вимірним вектором називають впорядковану сукупність із n- чисел і записують так а=(а1, а2,.....аn); а  (3.1)
(3.1)
Векторним простором називають множину елементами якої є вектори (3.1).
Лінійним векторним простором називають векторний простір в якому введені лінійні дії з векторами, а+b=(a1+b1, a2+b2,…..an+bn), які задовольняють властивостям:
1) переставний закон додавання a+b=b+a
2) сполучний закон (a+b)c=a(b+c)
3) існує нульовий вектор $0, такий, що а+0=а
4) існує протилежний вектор $(-а), такий, що а+(-а)=0
5) існує числовий множник 1, $1, такий, що 1а=а
6) a(a+b)=aa+ab
7)
| а11 а21 : ап1 |
8) a(ba)=(ab)a
Сукупність векторів а1, а2,…….аn (3.2),де аn = н називають лінійно
незалежними векторами, якщо 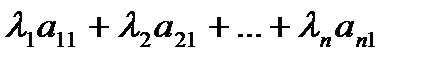 = 0 (3.3), при умові, що всі λi = 0 (3.4).
= 0 (3.3), при умові, що всі λi = 0 (3.4).
Якщо умова (3.3) виконується, а (3.4) не виконується, то вектори називають лінійно залежними. Вираз 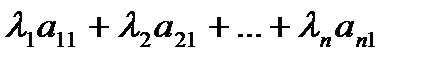 - називають лінійною комбінацією векторів.
- називають лінійною комбінацією векторів.
Розглянемо векторне рівняння (3.3) і запишемо його в скалярній формі
| 0 0 : 0 |
| а п 1 ап 2 : апп |
| а12 а22 : ап2 |
| а11 а21 : ап1 |
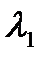 +
+ 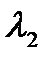 + … +
+ … + 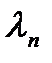 =
=
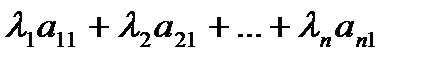 0
0
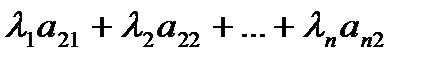 = 0
= 0
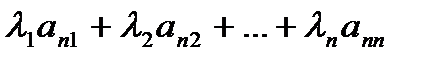 0
0
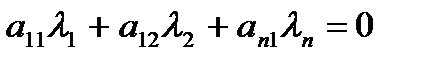 (3.5)
(3.5)
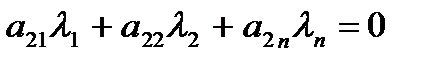
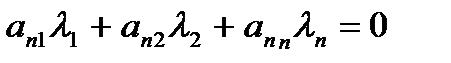
(3.1) векторне рівняння відносно невідомих 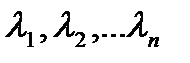 .
.
(3.4) скалярна система відносно невідомих 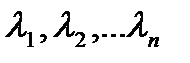 , тобто (3.3) і (3.5) – це одне й те саме рівняння тільки по різному записане.
, тобто (3.3) і (3.5) – це одне й те саме рівняння тільки по різному записане.
Розглянемо систему (3.5). Її називають однорідною системою рівнянь.
Зауваження: однорідна система завжди сумісна:
1) якщо 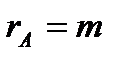 , то має єдиний розв’язок і він дорівнює
, то має єдиний розв’язок і він дорівнює 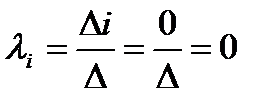 ,
, 

2) якщо 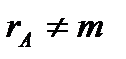 , то безліч розв’язків серед яких будуть ненульові.
, то безліч розв’язків серед яких будуть ненульові.
Висновок:
Вектори незалежні будуть в тому випадку, коли рані матриці
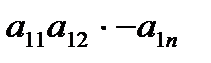
А= 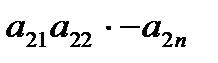 ,
, 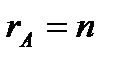 , тобто числу невідомих де n – число невідомих λi,
, тобто числу невідомих де n – число невідомих λi,
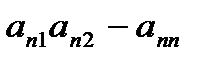
2. Базисом лінійного векторного простору називають сукупність векторів (3.2), якщо:
1) вектори лінійно-незалежні;
2) довільний вектор простору є їх лінійною комбінацією, де в1,в2…вn називають координатами вектора в в базисі (3.2).
Розмірністю лінійного векторного простору називають максимальне число можливих лінійно-незалежних векторів цього простору, якщо в просторі максимально можливих незалежних n векторів то говорять, що він розмірності n і записують так 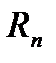
Приклад 3.
Перевірити чи вектори
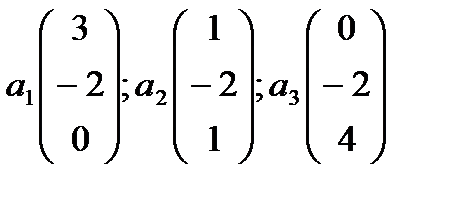
 лінійно незалежні.
лінійно незалежні.
Знайти координати вектора в = -1 в цьому базисі.
2
1
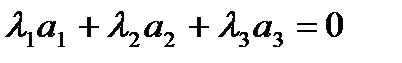
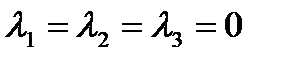
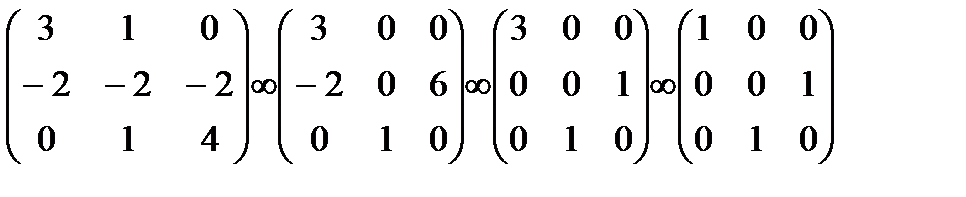
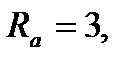 n=3
n=3 
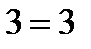
Рівняння має нульовий розв’язок, тому вектори лінійно-незалежні.
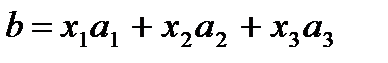
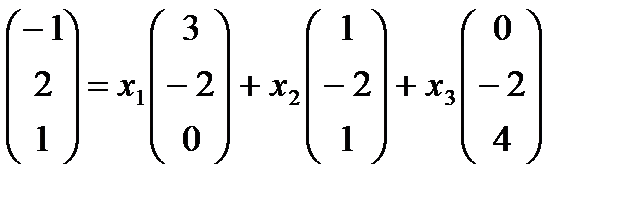
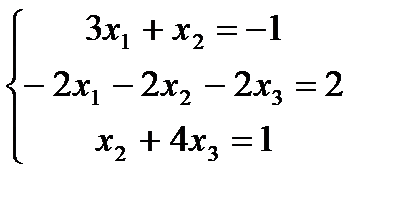
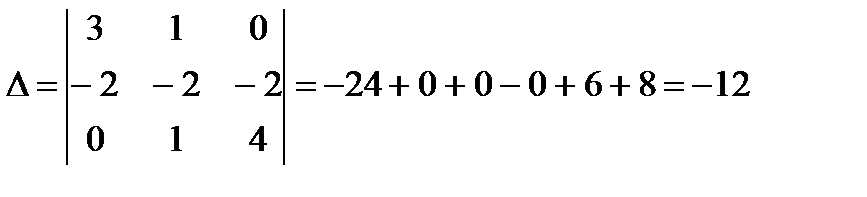
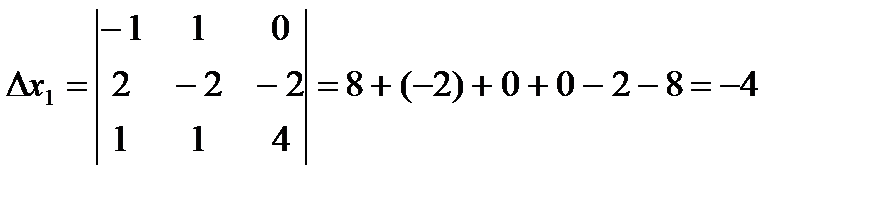
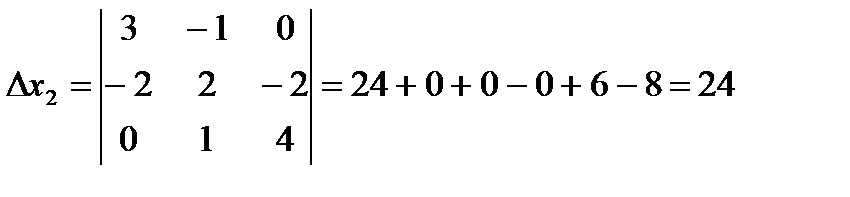
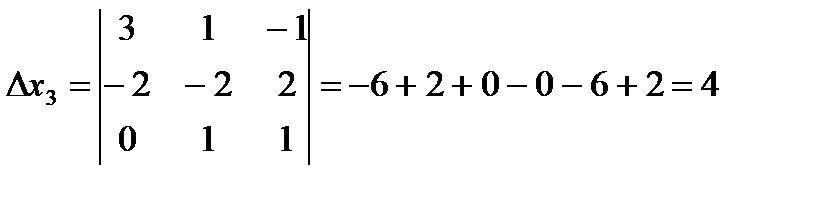
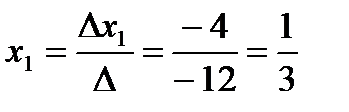
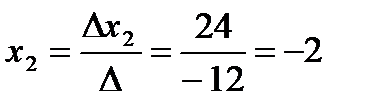
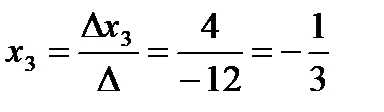
Відповідь: 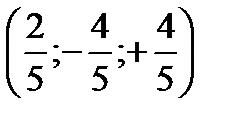
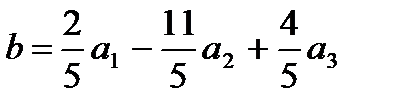
13
 2020-07-12
2020-07-12 102
102








