Визначники вищих порядків

     Визначником n-го порядку називають число, яке позначають:

   а₁₁ а₁₂ а_1n

   а₂₁ а₂₂   а_2n ≡ ∆

    … … …

    а_n1 а_n2 а_nn 

і обчислюють за формулою:

  ∆ = а_i1*A_i1 + a_i2*A_i2 +…+ a_in*A_{in            (1.6)}

 

Приклад 9.  Обчислимо визначник четвертого порядку:

 3 -2 4 0             3 -2 4 0                             3 -2 4

-3 1 -2 1 2  = -3 1 -2 1 = 1*А₂₄ = М₂₄ = -7 2 -1 =

-1 0 3 -2            -7 2 -1 0                             1 2 1

 4 1 2 -1              1 2 1 0                            -2

                                                                              -1     

3 -8 1

-7 16 6 = А₃₁ = М₃₁ = -8 1 = -48-16 = -64

1 0 0                           16 6

 

Матриці їх види дії з матрицями

6.  Матрицею розмірності nхm називають прямокутну таблицю з чисел:

   а₁₁ а₁₂ … а_1m

   а₂₁ а₂₂ … а_2m  

   … … …         A                                 (1.8)

    а_n1 а_n2 … а_nm 

 

 

Якщо n ≠ m, то матрицю називають прямокутною.

Символічний добуток числа рядків k на число стовпців n матриці nхm назиєвається розмірністю.

Види матриць:

1. Прямокутна

2. Квадратна

3. Транспонована

4. Кульова

5. Діагональна

6. Одинична

7. Симетрична

 

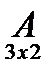 = 2 -3    = 2 -1 1 -3 = 1 -2 3  = 1

      0 4              0 4 0 2          0 1 4             2

      1 2                                           -1 2 0             0

Одиничною матрицею називається матриця, яка при множенні на одну матрицю не змінює її елементів.

1 0... 0 0                        

Е = 0 1... 0 0            Е: А*Е = Е*А = А                    (1.9)

0 0... 1 0

0 0 …0 1            

Множення матриць

Добутком АВ (m*n) – називається матриця С, яка дорівнює сумі добутків відповідних елементів і-го рядка матриці А та j-го стовпця матриці В.

=  , =          

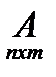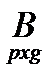m – кількість стовпців

p – кількість рядків

*  = =                              

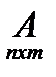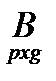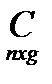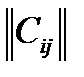
C_ij = a_i1 *b_1g +a_i2 *b_2g +…+a_im*b_mj             (1.10)

Приклад 13.

         3 4 5                        2 3

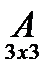 = 7 -2 1  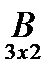        = 1 4

         0 3 -2                        2 7

                                 

                                   3*2 + 4*1 + 5*2        3*3 + 4*4 + 5*7 

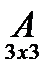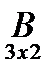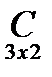 *  =  =   7*2 + (-2)*1 + 1*2   7*3 + (-2)*4 + 1*7 =

                                0*2 + 3*1 + (-2)*2   0*3 + 3*4 + (-2)*7

  20 60

= 14 20

  -1 -2

Додавання матриць

Сумою двох матриць однакових розмірів називається матриця такого самого розміру, елементи якої дорівнюють сумі відповідних елементів матриць, які додаються.

с_ij = a_ij + b_ij

 Із означення суми матриць випливає, що сума будь-якої матриці і нуль-матриці того самого розміру дорівнює даній матриці.

А+О=А; О+А=А

Приклад 14.

     4 5           -3 4                                        1 9

A = 7 8    B = 0 5 C = A + B        C =   7 13

    -1 0           -7 2                                        -8 2

 

Віднімання матриць

Різницею двох матриць однакових розмірів називається матриця такого самого розміру, елементи якої дорівнюють різницям відповідних елементів матриць зменшувального і від’ємника.

c_ij = a_ij - b_{ij    (1.11)}

Матриці А і В називаються протилежними, якщо їхня сума А+В=0 є нуль матриці.

Добуток матриці на число

Добутком матриці на число (або число на матрицю) називається матриця, елементами якої є добуток елементів даної матриці на число.

                      а₁₁ а₁₂... а_1n           λ а₁₁ λ а₁₂... λ а_1n

λА = Аλ = λ а₂₁ а₂₂ ... а_2n =  λ а₂₁ λ а₂₂ ... λ а_2n              (1.12)

                  а_m1 а_m2... а_mn          λ а_m1 λ а_m2... λ а_mn 

 

Операція множення матриці на число має розподільну властивість:

λ (А+В) = λА + λВ

 

Поняття оберненої матриці

Обернена матриця

Оберненою матрицею для даної матриці називається така матриця, яка будучи помножена на дану матрицю зліва або справа дорівнює одиничній матриці.

А^-1*А = А*А^-1 = Е – одинична матриця.       (1.13)

Теорема: Якщо матриця квадратна і невироджена det A ≠ 0, то вона має обернену,

яка знаходиться за формулою:

 

           А₁₁ А₁₂ А_1n    

А^-1= 1    А₂₁ А₂₂ А_{21                                                        (1.14)}

  det A А_n1 А_n2 А_nn

Правило знаходження оберненої матриці:

1. Знаходимо визначник матриці А: det A ≠ 0;

2. Знаходимо алгебраїчні доповнення всіх елементів матриці:

                                                   А₁₁ А₁₂ А₁₃

                                       A* =  А₂₁ А₂₂ А₂₃

                                                   А₃₁ А₃₂ А₃₃

 

3. Транспонуємо матрицю В:

                                                    А₁₁ А₂₁ А₃₁

                                           A = А₁₂ А₂₂ А₃₂

                                                    А₁₃ А₂₃ А₃₃

 

4. Ділимо матрицю A* на det A:

                                             А₁₁ А₂₁ А₃₁    

                          А^-1= 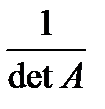       А₁₂ А₂₂ А₃₂

                                                  А₁₃ А₂₃ А₃₃

.

9.

Вектором називають величину, яка характеризується не тільки своїм числовим значенням (довжиною), але й напрямом, тобто геометрично – це напрямлений відрізок.

Вектори позначають а, в, с або АВ, СD.

Довжину (модуль) вектора позначають |а|, |АВ|

Нульовим вектором називають вектор початок і кінець якого співпадають.

Рівними називають вектори, які мають однакові довжини та напрямки.

Колінеарними називають вектори, які розташовані на одній прямій або паралельних прямих.

Протилежними називають колінеарні протилежно спрямовані вектори однакової довжини.

Координатами вектора називають проекції вектора на координатні осі.

а_х=|а| cos a, а_y=|а| cos b, а_z=|а| cos g, де cos a, cos b, cos g, називають напрямними косинусами вектора а.

Координати вектора М₁ М₂ дорівнюють різниці відповідних координат кінця та початку вектора.

Проекцією вектора АВ на вісь називається довжина вектора АВ_, яка взята із знаком “+”, якщо напрям АВ співпадає з напрямом осі та із знаком “-“, якщо напрями протилежні

а_х=пр_аха; а_y=пр_аyа; а_z=пр_аzа;

Модуль вектора АВ обчислюється за формулою:

d_АВ=Ö(х₁-х₂)²+(y₁-y₂)²+(z₁-z₂)²

Напрям вектора у просторі задають напрямні косинуси.

       Z     A

       а_z

       x            а_y  y       a = OA_z + OA_xy = OA_x + OA_y + OA_z

A_x                                                

    а_х             A_xy                     a = a_xi + a_yg + a_zk – це розклад вектора за ротами.

x

 

 

 

 

Таким чином аналітично вектор можна задати: а(а_x;а_y;а_z;) або а=a_xi+a_yg+a_zk.

 

10.

. Ортом вектора а називають вектор а, довжина якого дорівнює 1, а напрям співпадає з а, тобто а=|а|*а₀.

і(1;0;0)    орти або одиничний базис простору R₃.

g(0;1;0)

k(0;0;1)

 

4. Сумою двох векторів а та b називають вектор с, який сполучає початок вектора а з кінцем вектора b при умові, що початок вектора b вміщено в кінець вектора а.

Різницею двох векторів а та b будують як суму вектора а та вектора (-b).

Добутком вектора а на число к називають вектор b=к*а, колінеарний з вектором а, що має довжину в к раз більшу, ніж а та напрям такий самий як а, якщо к>0, і протилежний до а, якщо к<0.

Щоб помножити вектор а на число к, треба всі координати вектора помножити на число к, тобто

ка=(ка_1, ка_2,   ,ка_n, ).

Правило знаходження алгебраїчної суми векторів. Координати алгебраїчної скінченної кількості векторів дорівнюють такій же алгебраїчній сумі відповідних координат цих векторів..

а=(а₁, а₂,, а_n), b=(b₁, b₂,, b_n), с=(с₁, с₂,, с_n),

їх алгебраїчна сума а-b+с знаходиться за формулою:

а-b+с=(а₁-b₁+с₁, а₂-b₂+с₂,   , а_n-b_n+с_n);

12.

 Скалярним добутком векторів а та b називають число, яке дорівнює добутку модулів цих векторів на косинус кута g між ними.

Скалярний добуток векторів а та b позначають а*b або (а, b).

Отже згідно з означенням а*b=|а|*|b|*cosg.

Кутом між двома векторами (або між вектором та віссю) називають найменший кут між її напрямами при умові, що вектори зведено до спільного початку.

Знаходження скалярного добутку векторів а та b. Згідно з правилом множення матриць одержуємо

                           b₁

a*b(а₁, а₂, а₃)*  b₂ =a₁*b₁+a₂*b₊a₃*b₃,

                           b₃

 

тобто скалярний добуток двох векторів дорівнює сумі їх однойменних координат.

Якщо відомо координати векторів, то скалярний добуток знаходять за формулою:

a*b=a_x*b_x+a_y*b_y+...+a_z*b_z,

i*g=0                      a*a=|a|*|a|*cos 0⁰=|a|²,

i*i=1                                     a²=|a|²,

Умова перпендикулярності векторів:

a*b=0, бо cos 90⁰=0

Умова колінеарності векторів

a_x/b_x=a_y/b_y=a_z/b_z;

Приклад 1.

Дано: вектор а=3і-2у+к, b=-g+2r, c=2і-3d,

Знайти: 1) модуль вектора а, b, c; 2) напрямні косинуси для вектора а; 3) 2а-3b; b+с; 4) а скалярно помножити на b; 5) (2а-3b) (3b+c); 6) косинус j між а і b.

1) |a|=Ö3²+(-2)²+1²=Ö9+4+1=Ö14

|b|=Ö0²+(-1)²+4²=Ö5

|c|=Ö2²+(-3)²+0²=Ö13

2) Напрямні косинуси для вектора а:

cosa=а_х / |а|=3/Ö14»0,8, cosb=а_у / |а|=-2/Ö14»-0,5,

cosg=а_z / |а|=1/Ö14»0,3,

3) 2а-3b=2(3;-2;1)-3(0;-1;2)=(6;-4;2)-(0;-3;6)=(6-0;-4+3;2-6)=(6;-1;-4)

b+с=(0;-1;2)+(2;-3;0)=(2;-4;2)

4) а(3;-2;1), b(0;-1;2)

а*b=(3*0+(-2)*(-1)+1*2)=(0+2+2)=4

(2а-3b)*(3b+c)=(6;-1;-4)*(0;-3;6)+(2;-3;0)=(6;-1;-4)*(2+0;-4+(-3);6+0)=(6;-1;-4)*(2;-6;6)=(6*2+(-1)*(-6)+(-4)*6)=(12+6-24)=-6

5) Знайдемо cos j між а і b:

а*b=|а|*|b|cos j, звідси

cos j=а*b / |a|*|b|=(3;-2;1)*(0;-1;2) / Ö14*Ö5»4 / Ö70»0.5

cos j=0.5