2020-07-12
4973
Теорема (формула Остроградского-Лиувилля).
Пусть 
– частные решения ЛОДУ n-го порядка 
на 
. 
– определитель Вронского системы решений 
. Тогда
.
Док-во: (для случая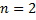 
)
ЛОДУ 2-го порядка: 
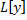– линейный дифференциальный оператор 2-го порядка.
Пусть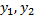 
– частные решения, тогда
Т.к. 
и 
– решения, то
,
,
,
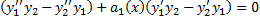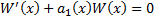Проинтегрируем от 
до 
:
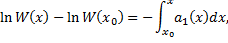
Следствие 1. Если 
, что 
, то 
Следствие 2 (Для ЛОДУ 2-го порядка).
Пусть 
– частное решение ЛОДУ 2-го порядка. Тогда функция
- частное решение ЛОДУ 2-го порядка причем 
образуют ФСР.
Док-во: по формуле Остроградского-Лиувилля
Считая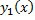 
известным, найдем 
такое, что
,
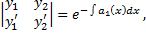
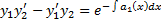
, значит 
.
Т.к. 
, то линейно независимы и образуют ФСР. 
Пример.
.
– частное решение, найти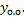 
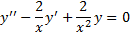
Тогда
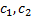– произвольные постоянные.
Теорема о структуре общего решения неоднородного ЛДУ n-го порядка. Теорема о наложении частных решений.
– линейный дифференциальный оператор с переменными коэффициентами 
Теорема (о структуре общего решения неоднородного ЛДУ n-го порядка).
|
|
|
Пусть 
– частное решение ЛНДУ 
. Тогда 
Док-во: нужно доказать, что 
такие, что функция 
– решение ЛНДУ, удовлетворяющее начальным условиям
.
Решение задачи Коши существует и определено на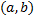 
в силу теоремы существования. Рассмотрим разность 
:
Т.е.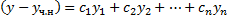 
– решение ЛОДУ; – ФСР ЛОДУ; 
Теорема (о наложении частных решений).
Пусть 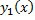– частное решение ЛНДУ; 
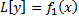; – частное решение ЛНДУ; 
. Тогда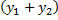 
– частное решение ЛНДУ 
Док-во: 
2.11. ЛОДУ с постоянным коэффициентами. Характеристическое уравнение и построение общего решения по его корням (вывод для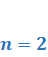 
).
,
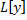– линейный дифференциальный оператор с постоянными коэффициентами:
.
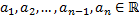Рассмотрим случай 
:
Для произвольного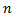 
найдем частное решение вида
.
.
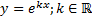Тогда
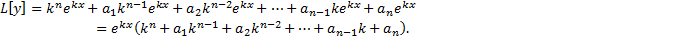
Опр. Уравнение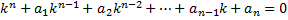 
называется характеристическим уравнением ЛОДУ с постоянными коэффициентами.
Таким образом, при 
имеем 
и функция является частным решением 
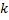является корнем его характеристического уравнения.
Построение ФСР ЛОДУ с постоянными коэффициентами по корням характеристического уравнения.
