Пусть  - различные корни характеристического уравнения. Тогда функции
- различные корни характеристического уравнения. Тогда функции

образуют ФСР ЛОДУ.
Док-во:
 – частные решения, т.к.
– частные решения, т.к.  - корни характеристического уравнения. Покажем, что
- корни характеристического уравнения. Покажем, что  – линейно независимы.
– линейно независимы.

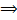
 – линейно независимы.
– линейно независимы.
(
При 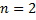 :
: 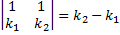 ).
).
Тогда  .
.
Пример.
 .
.
Характеристическое уравнение:
 ,
,
 ,
,
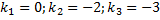 ,
,
 ,
,
 .
.
Случай кратных действительных корней.
Пусть 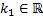 - корень кратности
- корень кратности 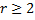 , т.е.
, т.е. 
 – многочлен, причем
– многочлен, причем 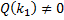 .
.
Корню  кратности
кратности 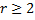 соответствует
соответствует 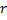 линейно независимых решений:
линейно независимых решений:




 .
.
Док-во: (для n=2)


Пусть 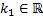 - корень кратности
- корень кратности  характеристического уравнения
характеристического уравнения
 .
.
Тогда по теореме Виета  .
.
 – решение, т.к.
– решение, т.к.  – корень.
– корень.
Покажем, что  – также решение:
– также решение:

 .
.
(
 ).
).
Тогда
 .
.
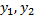 – решения, линейно независимые, т.к.
– решения, линейно независимые, т.к. 
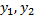 – ФСР ЛОДУ с постоянными коэффициентами 2-го порядка и кратным корнем
– ФСР ЛОДУ с постоянными коэффициентами 2-го порядка и кратным корнем  .
.

Пример.

Характеристическое уравнение:

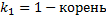 ,
,
 ,
,



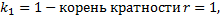
 .
.
ФСР:  .
.

Случай комплексных корней кратности 1.
Пусть 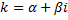 – корень характеристического уравнения кратности 1
– корень характеристического уравнения кратности 1  . Тогда
. Тогда 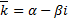 – также корень кратности 1. Паре корней
– также корень кратности 1. Паре корней  соответствуют 2 линейно независимых решения:
соответствуют 2 линейно независимых решения:

 .
.
Док-во:
Рассмотрим комплексную показательную функцию, которую введем по формуле Эйлера

Покажем, что  при
при 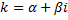 :
:
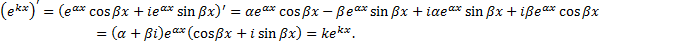
Тогда для функции 
 е.
е.  – комплексное решение ЛОДУ с постоянными коэффициентами.
– комплексное решение ЛОДУ с постоянными коэффициентами.
Т.к.  – решение, то
– решение, то  , т.е.
, т.е.  , т.е. функции
, т.е. функции
 ,
,

– решения ЛОДУ, они линейно независимы, т.к.  .
.
Примеры.
1.  .
.
 ,
,
 ,
,
 ,
,
 .
.
ФСР: 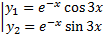 ,
,
 .
.
2.  .
.
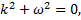

 ,
,
ФСР:  .
.
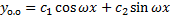 .
.
4. случай кратных комплексных корней (возможен только при 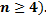
Пусть  – корни кратности
– корни кратности 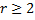 ,
,  . Им соответствуют
. Им соответствуют  линейно независимых решений:
линейно независимых решений:



 .
.
 2020-07-12
2020-07-12 636
636








