2020-07-12
1290
Размерность пространства решений ЛОДУ n-го порядка равна n.
Док-во: нужно доказать, что существует базис пространства решений, состоящий из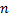 
частных решений, т.е. 
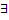частные решения 
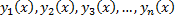, которые удовлетворяют следующим условиям:
1. Они линейно независимы на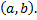 
2. Любое частное решение 
имеет вид 
1. рассмотрим частные решения ЛОДУ 
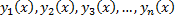, удовлетворяющие начальным условиям:
– фиксированная точка интервала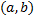 
.
По теореме существования и единственности решения задачи Коши 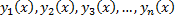определены на всем интервале .
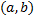Т.к. 
, то функции 
– линейно независимы на 
, т.к. иначе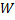 
должен был бы равняться нулю.
2. Рассмотрим произвольное частное решение 
.
Оно удовлетворяет некоторым начальным условиям:
Рассмотрим частное решение 
. Оно удовлетворяет начальным условиям:
Т.е. и 
удовлетворяют одинаковым начальным условиям в точке . По теореме о единственности решения 
Опр. Система n линейно независимых частных решений ЛОДУ n -го порядка называется фундаментальной системой решений (ФСР) ЛОДУ.
|
|
|
ФСР – базис линейного пространства решений.
Теорема о структуре общего решения ЛОДУ n-го порядка
Пусть 
– ФСР. Тогда общее решение имеет вид:
– произвольные постоянные.
Док-во: нужно доказать, что для 
такие, что частное решение 
удовлетворяет начальным условиям:
.
Решение , удовлетворяющее данным начальным условиям, существует и определено на всем .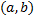 
линейному пространству решений и разлагается по базису линейного пространства:
