2020-08-05
62
Ряды Фурье. Рассмотрим ряд вида
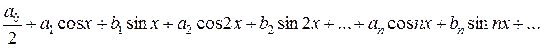
Этот ряд называется тригонометрическим, числа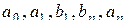 
- называют коэффициентами тригонометрического ряда или его можно записать в виде 
Допустим, что функция f (x) разлагается в тригонометрический ряд 
(49)
Если периодическая функция f(x) с периодом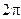 
является суммой равномерно сходящегося на 
тригонометрического ряда (49), то коэффициенты этого ряда определяются по формулам:
, 
, 
.
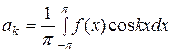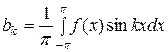Данные коэффициенты называют коэффициентами Фурье, а тригонометрический ряд 
, коэффициенты которого определяются по формулам Фурье, называю рядом Фурье.
Ряды Фурье для чётных и нечётных функций.
Если f (x) – чётная функция, её ряд Фурье содержит только свободный член и косинусы, т.е.
, где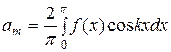 
.
Если требуется разложить в ряд Фурье нечетную функцию,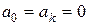 
, 
.
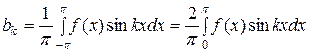Ряд Фурье для нечетной функции имеет вид: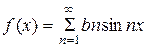 
.
Если функция f (x) – задана на 
, где l – произвольное число, то при выполнении на этом отрезке условий Дирихле указанная функция может быть представлена в виде суммы ряд Фурье:
,
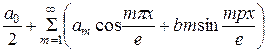где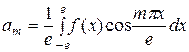 
, 
.
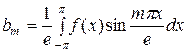Пример 104. Разложить в ряд Фурье функцию f(x) =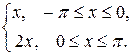 
определенную в интервале (- p; p).
Решение. Вычислим коэффициенты Фурье функции f(x).
а 0 = 
= 
+ 
=
= 
+ 
= - 
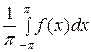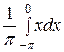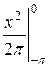+ p = .
а n =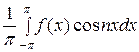 
= 
+
+ 
= 
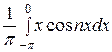(I1 + I2). Интегралы I1, I2 интегрируем по частям: I1 =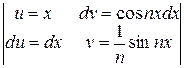 
= 
-
- 
= 
= 
.
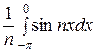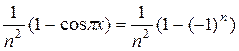I2 = 
= 
- 
= 
=
= 
= 
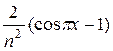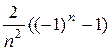. Итак, аn = 
+ 
=
= 
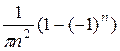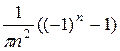. Аналогично вычисляем коэффициент bn:
bn =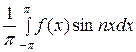 
= 
+ 
=
= 
= (
+ 
) +
+ 
(
+ 
) = (- 
- 
)= 
.
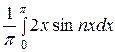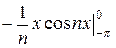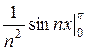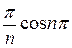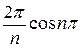Следовательно, ряд Фурье для функции f(x) имеет вид:
f(x) = 
+ 
.
