Практическая работа №7( 27.042020)

Тема: Вычисление определённого интеграла.

Цель выполнения задания: повторить знания о первообразной; закрепить навыки нахождения табличных интегралов; проверить уровень сформированности навыки нахождения первообразных; способствовать выработке вычислительных навыков; развивать логическое мышление, память, внимание и самостоятельность.

Обучающийся должен знать:

· символику и определение определённого интеграла;

· свойства определённого интеграла;

· методы интегрирования.

Обучающийся должен уметь: Вычислять определённый интеграл

 

Теоретическая часть.

Определённым интегралом называется предел интегральной суммы, когда длина отрезка стремится к нулю: lim f(x_i)Δx_i = 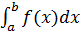. Для вычисления определённого интеграла применяется формула Ньютона- Лейбница:

                        = F(x) =F(b) – F(a)

Вычисление определённого интеграла с помощью табличных интегралов и его свойств называется непосредственным интегрированием.

Пример 1: 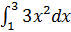 = x³ = 3³- 1³ =  8

Для вычисления определённого интеграла с помощью подстановки поступают так же, как и при вычислении неопределённого интеграла. Однако в этом случаи изменяют пределы интегрирования, и поэтому нет необходимости возвращаться к первоначальному аргументу.

 

Пример 2                              4x³+ 1 = t

                                                12x²dx = dt

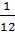
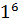        x²dx =              =  ⁵ dt=  =  ( - )=217

                                                tн = 40³+1 = 1

                                                tв = 41³+1=5

 

Практическая часть

Вычислить определённые интегралы:

1. ;

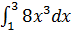2. 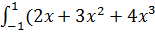+5x⁴) dx;

3. dx;

4. ;

5. ;

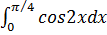6. ;

7. ;

8. ^x-1)⁴e^xdx;

9. ;

10.

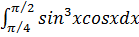
11.

12.

13.

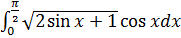
14.

15.

16.

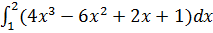
17.