2020-08-05
200
Практическая работа №1
Тема: Вычисление производной сложной функции
Цель выполнения задания: сформировать навыки вычисления производной сложной функции. Развивать логическое мышление, самостоятельность
Студент должен знать: символику и определение производной; второй производной; правила дифференцирования сложной функции.
Студент должен уметь: находить производную сложной функции.
Теоретическая часть.
Сложная функция- это функция от функции. Например, функция y= sin3x является сложной. Если обозначить 3x = u, то получим y = sin u, где u- промежуточная функция. В сложную функцию может входить не одна, а несколько промежуточных функций.
Производная сложной функции y по аргументу x равна производной функции по промежуточному аргументу u, умноженной на производную промежуточного аргумента u по основному аргументу x. y´ = y´u u´x.
Это правило иногда называют правилом цепочки. Оно остаётся справедливым и в случае, когда сложная функция состоит из любого конечного числа простых функций. Таким образом, производная сложной функции равна произведению производных от всех составляющих её функций. При этом следует помнить, что каждую функцию нужно дифференцировать по её собственному аргументу.
|
|
|
Например, продифференцировать функцию y = (x²+3x)5.
Составляющими функции являются y = u5, u = x² +3x. Согласно правилу дифференцирования сложной функции, находим
y´ = y´u u´ x = 5(x² + 3x)4(2x +3)
Практическая часть.
Найдите производные следующих функций: y = (9-x²)4, y =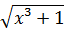 
,
y = ln sin3x, y = ln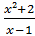 
, y = lncos³6x, y = 
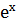sin2x, y= x³+cos²x, y = sin(x²-3x+5), y = sin² 5x, y = sin²3x - cos³4x, y = tglnx-ctg³x, y = (x4- 2x³-5x)6 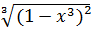y= 
y =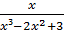 
, y=arctq(x²+3x), y= 
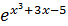, y=arccosx³
Практическая работа №2
Тема: Решение задач на определение оптимального решения
Цель выполнения задания: сформировать навык решения задач на нахождение оптимального решения, определение наибольших и наименьших значений реальных величин, развивать логическое мышление и внимание.
Обучающийся должен знать: правило нахождения наибольших и наименьших реальных величин с помощью производной.
Обучающийся должен уметь: находить наибольшее и наименьшее значение функции, непрерывной на интервале; решать несложные прикладные задачи на наибольших и наименьших значений реальных величин.
Теоретическая часть.
Для нахождения наибольшего и наименьшего значений функции, непрерывной в некотором промежутке, необходимо:
1) Найти производную функции и определить её критические точки, принадлежащие заданному интервалу, вычислить значение функции в этих точках;
|
|
|
2) Найти значение функции на концах промежутка;
3) Сравнить полученные значения и выбрать среди них наибольшее наименьшее значение функции в рассматриваемом промежутке.
Пример: Найти наименьшее и наибольшее значение функции f(x) =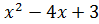 
в промежутке 0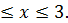 
Имеем f ´(x) = 2x – 4. Находим её критические точки. Для этого приравниваем производную к нулю, получаем 2x - 4 = 0. Решаем уравнение: x = 2 – это критическая точка. Находим f(2) = -1; далее вычисляем значения функции на концах промежутка: f (3) = 0, f (0) = 3.
Итак, наименьшее значение функции равно -1 и достигается ею во внутренней точке промежутка, а наибольшее равно 3 и достигается на левом конце промежутка.
Практическая часть.
1.Найти наибольшее наименьшее значение следующих функций:
f(x) = x²- 4x +3 на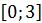 
f(x)= x³-3x²+3x+2 на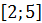 
f(x) = 3x4+4x³+1 на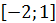 
2.Разложить число 100 на два слагаемых так, чтобы их произведение было наибольшим.
3.Требуется вырыть яму объёмом 32 м³, имеющую квадратное дно, так чтобы на облицовку её дна и стен пошло наименьшее количество материала. Каковы должны быть размеры ямы?
4.Оросительный канал имеет форму равнобокой трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон площадь сечения канала является наибольшей?
5.Тело движется по закону s = 18t +9t² - t³. Найти его максимальную скорость.
6.Из всех цилиндров с площадью полной поверхности s = 48π см² найти тот, который имеет наибольший объём.
