Теорема Ван Циттерта-Цернике

Определим взаимную интенсивность 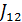 и степень когерентности  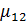для двух точек  и  экрана 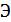, освещаемого протяженным немонохроматическим источником  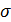(рис.9.9).

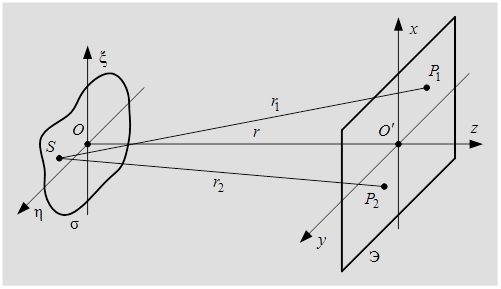
Рис. 9.9 – К расчёту взаимной интенсивности и степени когерентности для точек 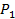 и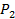

Для простоты в качестве 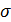 возьмем часть плоскости параллельной  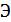и предположим, что среда между  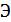и 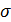 однородна. Допустим также, что малы как линейные размеры источника  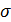по сравнению с расстоянием 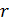, так и углы между прямыми 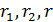. (S — произвольная точка источника 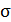). Процесс излучения источника будем считать стационарным.

Разобьём источник на элементы 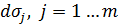 (линейные размеры элементов малы по сравнению с 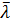) c центрами в точках 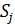. Есл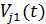и  и 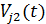 — комплексные возмущения в точках  и , обусловленные одним элементом 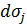, то общее возмущение (аналитические сигналы) в этих точках равны

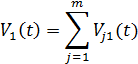
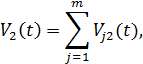
следовательно, взаимная интенсивность в этих точках, согласно определению (9.71)

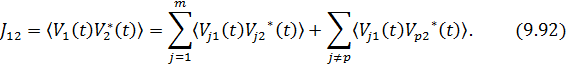
Вторая сумма в (9.92) равна нулю, поскольку возмущения, создаваемые в  и  разными статистически независимыми элементами источника, некогерентны и средние значения возмущений .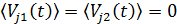

Пусть комплексная амплитуда колебаний источника в 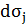 равна 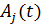, тогда очевидно

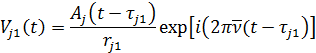
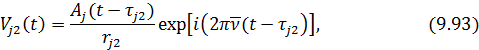
где 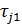 и 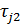- времена запаздывания, определяемые выражениями

где 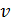 — скорость распространения волны в среде. Следовательно

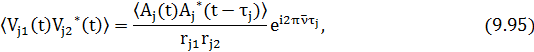
где 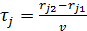 — относительное время запаздывания.

Отметим, что последнее равенство в (9.95) возможно в силу сделанного предположения о стационарности процесса излучения.

Поскольку 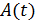 — медленно меняющаяся функция, то можно полагать, что  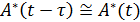и тогда (9.92) с учетом (9.95) примет вид:

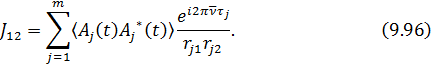
Величина 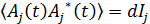 — представляет собой интенсивность излучения площадки  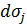источника. Обозначим площадь  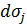через 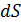 и поверхностную плотность излучения источника (яркость) 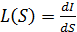. Получим, переходя в (9.96) к интегрированию

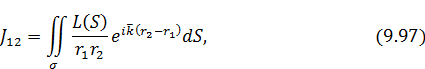
где 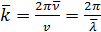 — волновое число для средней частоты  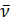(длины волны 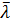) квазимонохроматического источника.

Комплексная степень когерентности

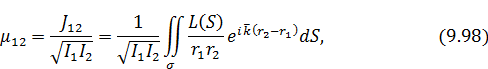
где

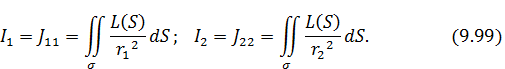
Отметим, что, если 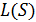 трактовать как яркость элемента 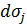, то с фотометрической точки зрения интенсивност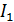и  и 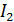, в силу сделанных допущений, представляют собой освещенности в  и  от источника .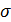

Формула (9.98) впервые была получена Ван Циттертом и Цернике. Видно, что с точностью до постоянного коэффициента она напоминает дифракционный интеграл в расчете поля в точке  , если на отверстие 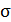 падает сферическая волна, сходящаяся в точке . (Рис. 9.10)

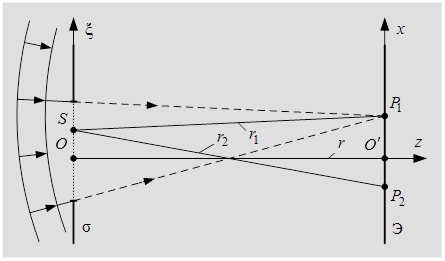
Рис. 9.10 – К вычислению дифракции в точке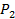

Как известно, если на отверстие 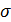 падает сферическая волна с центром в точке , то поле в точке  определяется выражением:

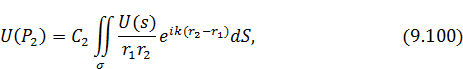
где 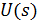 — поле на отверстии 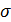;  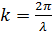— волновое число;  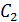— комплексная постоянная.

Несомненное сходство интегралов (9.98) и (9.100) позволило Ван Циттерту и Цернике сформулировать следующее правило.

Теорема Ван Циттерта-Цернике:

Комплексная степень когерентности, которая описывает степень когерентности колебаний в точках P₁ и P₂ плоскости, освещённой протяженным квазимонохроматическим источником равна нормированной комплексной амплитуде в точке P₂ некоторой дифракционной картины с центром в точке P₁. Эта картина получится, если заменить источник дифракционным отверстием такого же размера и формы и заполнить его сферической волной, сходящейся в точке P₁, причем распределение амплитуд по волновому фронту в отверстии должно быть пропорциональным интенсивности (яркости) по источнику.

Теорема Ван Циттерта - Цернике имеет большое практическое значение. Она позволяет рассчитать степень пространственной когерентности от немонохроматического протяженного источника без использования операции временного усреднения аналитических сигналов в точках  и .

В большинстве приложений можно считать, что яркость 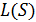 не зависит от положения точки  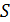(равнояркий источник). Тогда расчёт комплексной амплитуды в точке  сводится к расчёту дифракции волны постоянной амплитуды на отверстии такого же размера и формы как и источник. Пусть 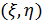 — координаты произвольной точки  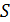источника, а 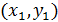,  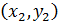координаты точек  и  в плоскости 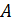 (рис.9.9). Тогда имеем очевидные соотношения:

.

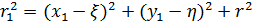
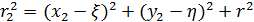Откуда в силу сделанных допущений находим:

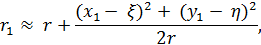
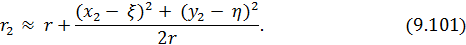
В знаменателе подынтегральных выражений (9.98) и (9.100) 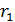 и 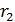 можно заменить на 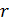. Разность расстояний  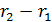в экспоненте будет равна:

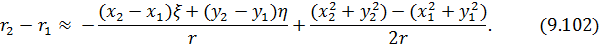
Обозначим

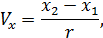
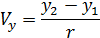
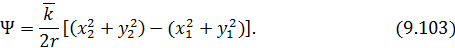
Тогда (9.98) примет вид:

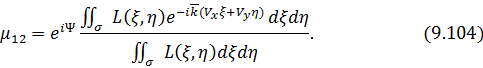
Это означает, что если размеры источника малы по сравнению с расстоянием до точек  и , то степень когерентности равна нормированному преобразованию Фурье от функции, описывающей яркость источника, а знаменатель в (9.104) представляет собой его силу света.

Величина 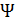 также имеет простое толкование. Для центральной точки  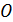источника  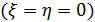величина  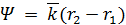равна разности фаз колебаний  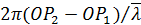в точках  и . Если 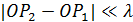 этой величиной можно пренебречь.

Для равнояркого круга радиуса 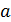 из (9.104) получим (см. главу 7, дифракцию Фраунгофера на круге):

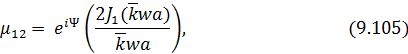
где 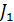 — функция Бесселя первого рода первого порядка,

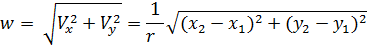
— угловое расстояние между  и .

График функции 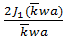 приведён на рисунке 9.11. Можно считать, что это график  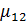при .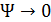

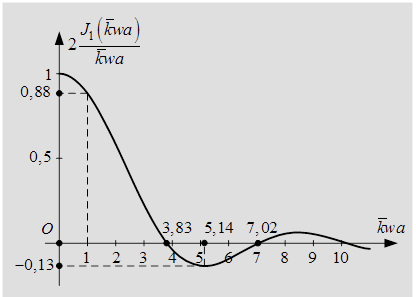
Рис.9.11 – График функции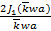

Из графика видно, что степень когерентности от максимального значения равного единице монотонно уменьшается до значения 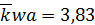, при котором 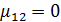. В этом случае точки  и  находятся на расстоянии:

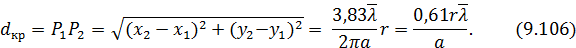
При дальнейшем увеличении 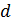 вновь наступает небольшая когерентность, но её степень остаётся меньше .

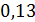Полная некогерентность вновь наступает при 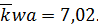 Проходя через нуль, функция Бесселя каждый раз меняет знак. Это значит, что фаза  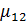меняется на 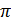, следовательно, после исчезновения полос (переход через нуль) светлые и тёмные полосы меняются местами (обращение контраста). При  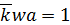значение функции  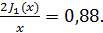Это соответствует расстоянию между точками  и :

Считая отклонение в 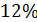 вполне допустимым отклонением от идеального значения, на основании (9.107) можно считать, что равнояркий квазимонохроматический источник с угловым размером  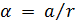почти когерентно освещает площадку в виде круга диаметром

Оценим величину 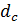 на земной поверхности, освещаемой Солнцем. Если считать Солнце равноярким диском с угловым размером
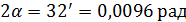, то для средней длины волны  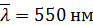получаем

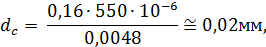
т.е. размер когерентно освещаемой области незначителен.