2020-08-05
99
Общие соотношения
Снова обратимся к комплексной функции взаимной когерентности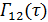 
, введённой нами в разделе 9.3. Как там отмечалось, эта функция определяет не только пространственную, но и временную когерентность волн, проходящих из точек 
и 
в зависимости от времени относительной задержки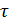 
. Напомним, что эта функция может быть записана в виде:
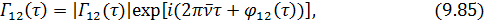
где модуль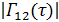 
и модуляция фазы 
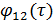медленно меняющиеся функции по сравнению с 
.
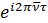Отмеченное обстоятельство позволяет во многих практических случаях при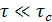 
пренебречь влиянием медленно меняющихся функций и представить (9.85) в виде
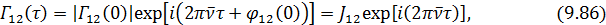
где
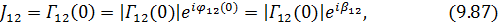
функция взаимной интенсивности. Аргумент этой функции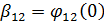 
.
Введенная функция может быть выражена через аналитические сигналы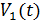 
и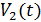 
в точках и
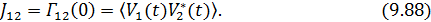
Она характеризует пространственную когерентность колебаний в этих точках.
При сделанных допущениях можно аналогичным образом преобразовать степень взаимной когерентности, а именно
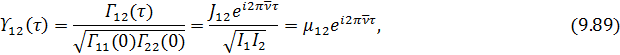
где
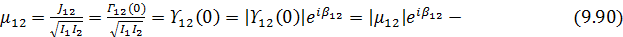степень взаимной интенсивности, также характеризующая пространственную когерентность в точках и .
Таким образом, при условии 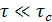, т.е. в окрестности точек максимального интерференционного контраста во всех соотношениях раздела 3 вместо функци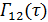й и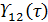 
можно произвести замены
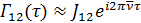
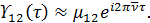
В частности, закон интерференции (9.15) запишется в виде:
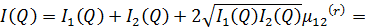
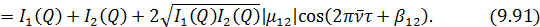
Здесь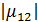 
заключен в пределах 
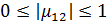и характеризует максимально возможный контраст интерференционной картины.
Расчёт взаимной интенсивности и степени когерентности.
