Майкельсон в 1890 г. предположил схему интерферометра, позволяющего определять угловые размеры астрономических объектов, (рис.9.12).
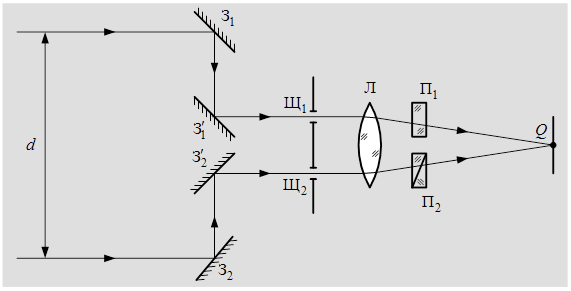
Рис.9.12 – Схема звёздного интерферометра Майкельсона
Свет от звезды падает на два зеркала  и
и  и с помощью зеркал
и с помощью зеркал  и
и 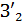 направляется на две щели
направляется на две щели 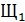 и
и 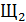 , находящиеся перед объективом
, находящиеся перед объективом 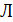 . В заднем фокусе объектива (в точке
. В заднем фокусе объектива (в точке 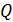 ) происходит наложение интерферирующих пучков. Пластинка
) происходит наложение интерферирующих пучков. Пластинка 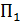 предназначена для сведения пучков в одну точку, а пластинка
предназначена для сведения пучков в одну точку, а пластинка 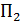 (переменной толщины) для компенсации неравенства оптических путей. Эта компенсация необходима, т.к. полосы в белом свете видны только в области нулевого порядка (при условии
(переменной толщины) для компенсации неравенства оптических путей. Эта компенсация необходима, т.к. полосы в белом свете видны только в области нулевого порядка (при условии 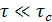 ). Расстояние между зеркалами
). Расстояние между зеркалами 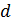 может изменяться путём механического перемещения. Если
может изменяться путём механического перемещения. Если 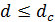 для выбранной звезды, то контраст интерференционной картины близок к единице. При дальнейшем увеличении
для выбранной звезды, то контраст интерференционной картины близок к единице. При дальнейшем увеличении 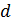 контраст уменьшается и при
контраст уменьшается и при 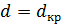 становится равным нулю. Значение
становится равным нулю. Значение 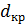 по (9.106) позволяет определить угловой размер
по (9.106) позволяет определить угловой размер 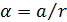 звезды. По теории, при
звезды. По теории, при 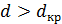 снова возникает интерференция с малым и обращенным контрастом, однако из-за влияния турбулентности атмосферы эта область практически не использовалась. Первой звездой, угловые размеры которой были измерены, была Бетельгейзе (
снова возникает интерференция с малым и обращенным контрастом, однако из-за влияния турбулентности атмосферы эта область практически не использовалась. Первой звездой, угловые размеры которой были измерены, была Бетельгейзе (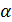 Ориона). Полученная величина оказалась равной
Ориона). Полученная величина оказалась равной 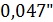 . Измеренная величина
. Измеренная величина 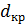 составила
составила 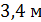 .
.
Максимальная величина 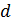 , построенного Майкельсоном интерферометра, была равной
, построенного Майкельсоном интерферометра, была равной 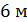 , поэтому Майкельсон смог определить угловые размеры сравнительно небольшого количества звезд, для которых
, поэтому Майкельсон смог определить угловые размеры сравнительно небольшого количества звезд, для которых 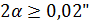 . Тем не менее интерференционный метод Майкельсона измерения диаметров небесных тел был очень весомым вкладом в астрономическую науку, поскольку во много раз превышал возможности оптических телескопов того времени.
. Тем не менее интерференционный метод Майкельсона измерения диаметров небесных тел был очень весомым вкладом в астрономическую науку, поскольку во много раз превышал возможности оптических телескопов того времени.
Рассмотрение в настоящей главе основ теории интерференции и дифракции частично когерентного света имеют большое познавательное и практическое значение. Эта теория восполняет пробел между волновыми явлениями когерентного и некогерентного света, наблюдающийся во многих пособиях по физической оптике. Отмеченные здесь примеры практического использования этой теории: определение угловых размеров небесных тел и Фурье-спектроскопия – являются лишь малой частью уже реализованных и перспективных её возможностей.
К сожалению, формат учебного пособия и его назначение не позволяют отразить в нём все особенности интерференции и дифракции от протяжённых квазимонохроматических источников. Для более глубокого изучения волновых свойств частично когерентного света, поляризации, образования изображения и других, советуем читателю обратиться к специальным монографиям и пособиям [1,3,5], где эти вопросы рассматриваются в более широком аспекте как с точки зрения используемого математического аппарата, так и многообразия областей проявления свойств частично когерентного света.
Задачи и примеры
Задача 1. Комплексная функция взаимной когерентности в точках  и
и 
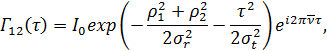
где 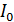 — некоторый постоянный коэффициент;
— некоторый постоянный коэффициент; 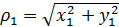 ,
,
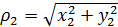 — полярные координаты точек
— полярные координаты точек  и
и  , а
, а 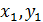 ;
; 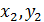 — их координаты;
— их координаты; 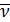 — центральная частота квазимонохроматического источника;
— центральная частота квазимонохроматического источника;
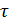 — относительная задержка колебаний в точках;
— относительная задержка колебаний в точках; 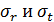 — коэффициенты, определяющие области пространственной и временной когерентности. Для точек
— коэффициенты, определяющие области пространственной и временной когерентности. Для точек  и
и  с заданными координатами
с заданными координатами 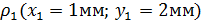 ,
,
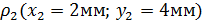 ,
, 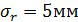 ,
, 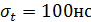 ,
, 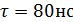 и произвольной
и произвольной 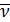 определить:
определить:
a) интенсивности 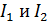 .
.
b) степень взаимной когерентности 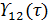 и значение её модуля.
и значение её модуля.
c) взаимную интенсивность 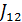 и степень когерентности
и степень когерентности 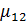 .
.
Решение: По определению интенсивности 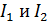 равны
равны
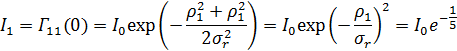
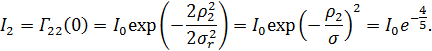
a) Степень взаимной когерентности:
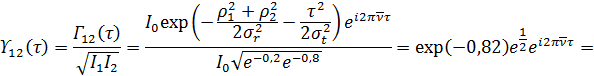
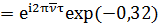
поэтому 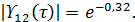
b) Взаимная интенсивность
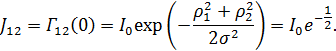
Степень когерентности 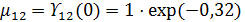 .
.
Задача 2. В интерферометре, работающем по методу деления амплитуды, интерферируют два квазимонохроматических пучка с интенсивностями
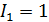 ,
, 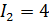 . Определить контраст интерференционной картины в области наложения пучков, если модуль степени когерентности пучков
. Определить контраст интерференционной картины в области наложения пучков, если модуль степени когерентности пучков 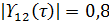 .
.
Решение: Интенсивность при интерференции квазимонохроматических пучков описывается выражением:
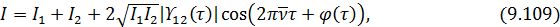
где 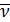 — центральная частота света;
— центральная частота света; 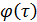 — девиация фазы.
— девиация фазы.
Контраст интерференционной картины:

Из (9.109) следует, что
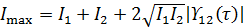
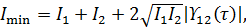
поэтому из (9.110) находим:
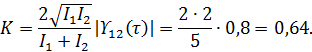
Задача 3. Спектральная плотность яркости источника света в интерферометре Майкельсона представляет собой совокупность двух монохроматических компонент с частотами 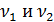 и равной интенсивности. При этом
и равной интенсивности. При этом 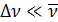 , где
, где
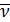 — центральная частота:
— центральная частота: 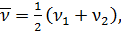
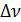 — разность частот
— разность частот 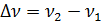 . Определить интерферограмму, регистрируемую приемником излучения при перемещении одного из зеркал интерферометра. Считать, что интенсивности
. Определить интерферограмму, регистрируемую приемником излучения при перемещении одного из зеркал интерферометра. Считать, что интенсивности 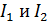 света от двух ветвей интерферометра одинаковы:
света от двух ветвей интерферометра одинаковы: 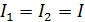 .
.
Решение: Интерферограмма представляет собой зависимость сигнала приемника излучения (т.е. интенсивности света) от смещения зеркала. В данном случае эта зависимость имеет вид:
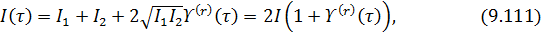
где 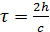 — относительная временная задержка колебаний (
— относительная временная задержка колебаний (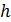 — смещение зеркала,
— смещение зеркала, 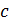 — скорость света).
— скорость света).
Спектральную плотность мощности источника представим в виде:
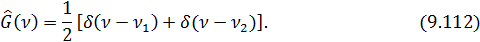
Это возможно, т.к.
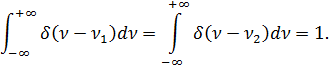
Используем связь между степенью собственной когерентности и функцией 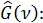
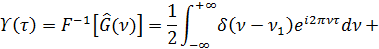
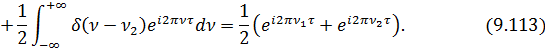
Последнее равенство в (9.113) получено на основании использования известного фильтрующего свойства 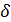 — функции, а именно:
— функции, а именно:
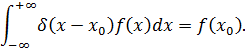
Из (9.113) имеем:
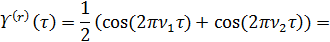
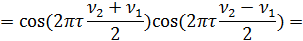
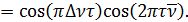
Окончательно из (9.111) получаем:
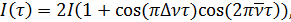
где 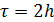 .
.
График этой функции при 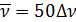 представлен на рисунке 9.13. Его полезно сравнить с графиками на рисунках 9.8 а),б),в).
представлен на рисунке 9.13. Его полезно сравнить с графиками на рисунках 9.8 а),б),в).
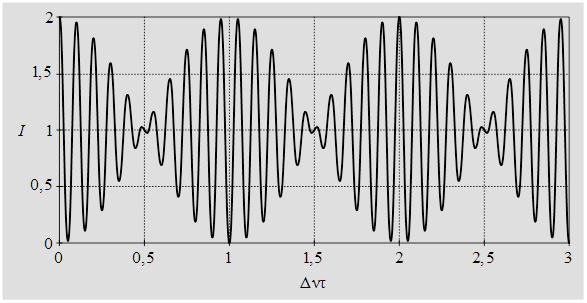
Рис. 9.13 – График интерферограммы
Задача 4. В Фурье спектрометре при перемещении одного из зеркал зарегистрирована интерферограмма 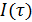 , переменная составляющая которой имеет вид:
, переменная составляющая которой имеет вид:
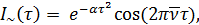
где 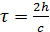 ;
; 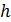 — смещение зеркала;
— смещение зеркала; 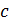 — скорость света;
— скорость света; 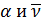 — константы. Определить спектральную плотность яркости источника, ширину его спектра, оценить время когерентности.
— константы. Определить спектральную плотность яркости источника, ширину его спектра, оценить время когерентности.
Решение: Спектральная плотность мощности источника с точностью до несущественной постоянной определяется следующим образом:
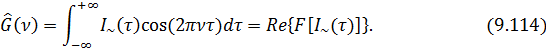
Используем известное свойство Фурье преобразования:
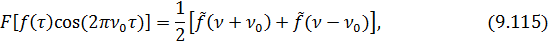
где 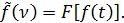 В нашем случае
В нашем случае 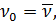
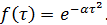 Преобразование Фурье этой функции известно.
Преобразование Фурье этой функции известно.
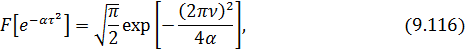
поэтому с учетом (9.115) из (9.114) получаем:
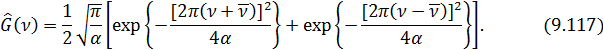
Эта функция представляет собой сумму двух идентичных функций, симметричных относительно нулевой частоты 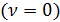 , одна из которых с центром
, одна из которых с центром 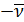 располагается в области отрицательных частот, а другая с центром
располагается в области отрицательных частот, а другая с центром 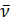 — в области положительных частот. Первая из этих функций не имеет физического смысла, поэтому окончательно для спектральной плотности яркости
— в области положительных частот. Первая из этих функций не имеет физического смысла, поэтому окончательно для спектральной плотности яркости 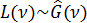 получаем:
получаем:
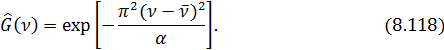
График этой функции приведен на рисунке 9.14
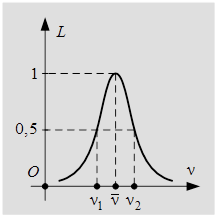
Рис.14 – Спектральная плотность яркости квазимонохроматического источника
Максимальное значение 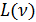 достигает в точке
достигает в точке 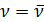 , где
, где 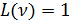 . Для нахождения ширины спектра найдем полуширину
. Для нахождения ширины спектра найдем полуширину 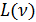 на уровне
на уровне 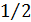 . Для этого решим уравнение:
. Для этого решим уравнение:
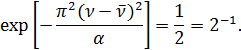
Отсюда имеем:
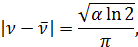
Корни этого уравнения
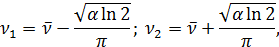
следовательно ширина спектра источника на уровне 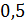 :
:
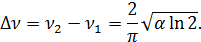
Последнее выражение даст возможность оценить время когерентности источника.
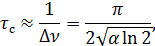
Примечание:
Более точное значение 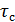 можно получить на основании раздела 9.4.2 главы. Так как функция
можно получить на основании раздела 9.4.2 главы. Так как функция 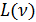 представляет собой гауссоиду, то
представляет собой гауссоиду, то
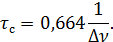
Задача 5. Две точки  и
и  освещаются квазимонохроматическим равноярким источником
освещаются квазимонохроматическим равноярким источником 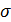 в виде полосы шириной
в виде полосы шириной 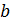 (рис. 9.15).
(рис. 9.15).
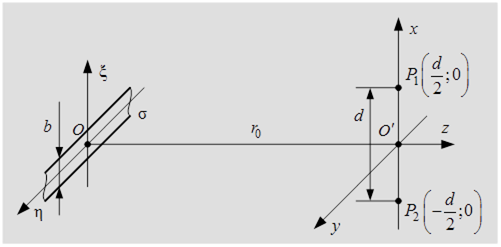
Рис. 9.15 – К расчёту степени когерентности 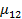
Координаты точек в плоскости 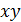 :
:
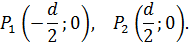
Расстояние между плоскостями 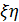 источника и
источника и 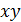 равно
равно 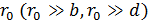 .
.
Центральная длина волны источника 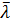 . Определить комплексную степень когерентности колебаний
. Определить комплексную степень когерентности колебаний 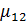 в точках
в точках  и
и  , расстояние
, расстояние 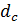 между точками, при котором
между точками, при котором 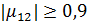 и расстояние
и расстояние 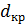 , при котором
, при котором 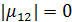 .
.
Решение: По теореме Ван Циттерта-Цернике:
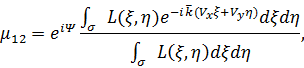
где 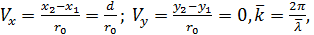
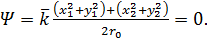
Поэтому:
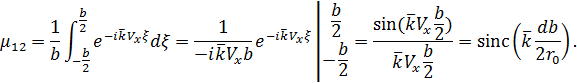
Расстояние 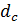 , в пределах которого точки
, в пределах которого точки  и
и  освещаются практически когерентно, найдем из условия:
освещаются практически когерентно, найдем из условия:
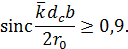
Решение этого неравенства имеет вид:
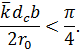
Откуда
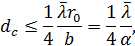
где 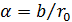 — угловой размер ширины источника.
— угловой размер ширины источника.
По определению
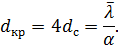
Как следует из вида функции 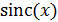 при значении
при значении 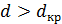 степень когерентности
степень когерентности 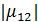 снова становится больше нуля, однако её значение не превышает
снова становится больше нуля, однако её значение не превышает 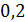 .
.
 2020-08-05
2020-08-05 453
453








