Кольцо многочленов от нескольких переменных

ГРУППОИД

- универсальная алгебра с одной бинарной операцией. Г.- самый широкий класс таких алгебр; группы, полугруппы, квазигруппы - все это Г. специального вида. Важным понятием для Г. является понятие изотоп и и операций. Пусть на множестве Gопределены две бинарные операции, обозначаемые (Х) и (о), они изотопны, если существуют такие три взаимно однозначных отображения 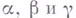множества Gна себя, что 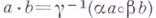для любых 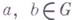. Г., изотопный квазигруппе, сам является квазигруппой; Г. с единицей, изотопный группе, изоморфен этой группе. Поэтому понятием изотонии в теории групп не пользуются, для групп изотония совпадает с изоморфизмом.

Группоид с сокращением - это Г., в к-ром любое из равенств 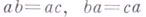влечет (а, 6, с - элементы Г.). Каждый Г. с сокращением вложим в квазигруппу. Гомоморфный образ квазигруппы - группоид с делением, т. е. Г., в к-ром уравнения 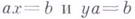разрешимы (но не обязательно однозначно).

Множество с одной частичной (т. е. определенной не для всяких пар элементов) бинарной операцией наз. частичным группоидом. Каждый частичный подгруппоид свободного частичного Г. свободен.

Магма (группоид) в общей алгебре — алгебра, состоящая из множества М с одной бинарной операцией M × M → M. Помимо требования замкнутости множества относительно заданной на нём операции, других требований к операции и множеству не предъявляется.

Термин «магма» был предложен Бурбаки. Термин «группоид» старше, он предложен Ойстином Оре, однако этот термин также относится к другой общалгебраической структуре — теоретико-категорному группоиду, и в более современной литературе чаще используется в этом смысле.

Типы магм

Как таковые магмы обычно не изучаются; вместо этого изучаются различные типы магм, отличающиеся дополнительно вводимыми аксиомами. Обычно изучаемые типы магм включают следующие:

квазигруппа — непустая магма, в которой всегда возможно деление;
петля или лупа — квазигруппа с нейтральным элементом;
полугруппа — магма с ассоциативной операцией;
моноид — полугруппа с нейтральным элементом;
группа — моноид с обратным элементом или, что то же, ассоциативная петля (всегда являющаяся квазигруппой);
абелева группа — группа с коммутативной операцией.

ПОЛУГРУППА

В математике полугруппой называют множество с заданной на нем ассоциативной бинарной операцией 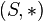. Существуют разногласия по поводу того, нужно ли включать требование непустоты в определение полугруппы; отдельные авторы даже настаивают на необходимости наличия нейтрального элемента («единицы»). Однако более общепринятым является подход, согласно которому полугруппа не обязательно является непустой и не обязательно содержит нейтральный элемент. Полугруппа с нейтральным элементом называется моноидом. Следует отметить, что любую полугруппу , не содержащую нейтральный элемент, можно превратить в моноид, добавив к ней некоторый элемент 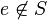и определив 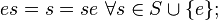полученный моноид обычно обозначается как .

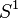Примеры полугрупп

Положительные целые числа с операцией сложения.
Любая группа является также и полугруппой.
Идеал кольца всегда является полугруппой относительно операции умножения.
Множество всех отображений множества в себя с операцией суперпозиции отображений.
Множество всех бинарных отношений на множестве с операцией умножения бинарных отношений.
Множество всех слов над некоторым алфавитом с операцией конкатенации (присоединения)

3. ГРУППА

Гру́ппа в математике — множество элементов с определённой на нём ассоциативной бинарной операцией, унарной операцией взятия обратного элемента и выделенным нейтральным элементом, связанное некоторыми естественными свойствами — групповыми аксиомами^[^⇨]. Ветвь общей алгебры занимающаяся группами, называется теорией групп.

· Наиболее известный пример группы — множество целых чисел, снабжённое операцией сложения: сумма любых двух целых также даёт целое число, число с противоположным знаком даёт обратный элемент, а роль нейтрального элемента играет нуль. Другие примеры — множество вещественных чисел с операцией сложения, множество вращений плоскости вокруг начала координат.

Непустое множество 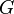с заданной на нём бинарной операцией 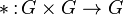называется группой 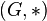, если выполнены следующие аксиомы:

ассоциативность: ;
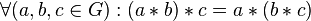наличие нейтрального элемента: ;
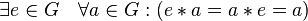наличие обратного элемента:

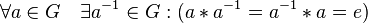
Примеры

Целые числа с операцией сложения. 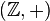— коммутативная группа с нейтральным элементом 0.

Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность и единица.

Свободная группа с двумя образующими (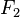) состоит из пустого слова, которое мы обозначаем (это единица нашей группы), и всех конечных слов из четырёх символов 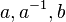и 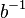таких, что 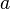не появляется рядом с 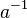и 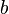не появляется рядом с 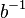. Операция умножения таких слов — это просто соединение (конкатенация) двух слов в одно с последующим сокращением пар 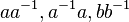и .

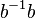Симметрическая группа. Множество всех биекций конечного множества в себя с операцией композиции является конечной группой, которая называется симметрической группой, или группой перестановок. Любая конечная группа является подгруппой некоторой симметрической группы (теорема Кэли).

Циклические группы состоят из степеней 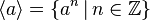одного элемента a. Такие группы всегда коммутативны. Примеры таких групп — упомянутые уже целые числа по сложению и группа корней из единицы.

Группа кубика Рубика — подгруппа симметрической группы S₄₈, элементы которой соответствуют движениям кубика Рубика. Композиция двух движений снова является движением, для каждого движения существует обратный элемент, имеется ассоциативность и нейтральный элемент.

КОЛЬЦО

Определение

Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами, выполняющимися для любых :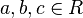

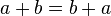— коммутативность сложения;
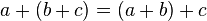— ассоциативность сложения;
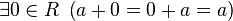— существование нейтрального элемента относительно сложения;
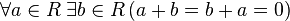— существование противоположного элемента относительно сложения;
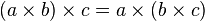— ассоциативность умножения;
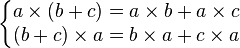— дистрибутивность.

Иными словами, кольцо — это универсальная алгебра 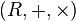, такая что алгебра 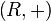— абелева группа, и операция дистрибутивна слева и справа относительно .

Кольца могут обладать следующими дополнительными свойствами:

наличие единицы: 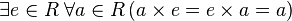(кольцо с единицей);
коммутативность умножения: 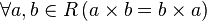(коммутативное кольцо);

Иногда под (ассоциативным) кольцом понимают кольцо с единицей. Но имеются примеры колец без единицы. Легче всего их построить как идеалы в кольце, не содержащие ненулевых идемпотентов, например кольцо чётных чисел, или многочленов степени 1 и выше.

Простейшие свойства

Непосредственно из аксиом кольца можно вывести следующие свойства:

Нейтральный элемент относительно сложения в кольце единственен. Для любого элемента кольца обратный к нему по сложению элемент единственен.
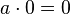, то есть 0 — поглощающий элемент по умножению.
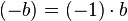, где 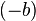— элемент, обратный к 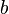по сложению.

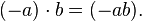
Примеры

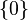— тривиальное кольцо, состоящее из одного нуля. Это единственное кольцо, в котором ноль является мультипликативной единицей. Этот тривиальный пример полезно считать кольцом с точки зрения теории категорий, так как при этом в категориях колец возникает терминальный объект.
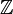— целые числа (с обычным сложением и умножением). Это важнейший пример кольца, так как любое кольцо можно рассматривать как алгебру над 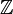. Также это начальный объект в категории Ring колец с единицей.
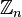— кольцо вычетов по модулю натурального числа n. Это классические примеры колец из теории чисел. Кольцо вычетов является полем тогда и только тогда, когда число n простое. Соответствующие поля являются отправной точкой для построения теории конечных полей. Кольца вычетов также важны при исследовании структуры конечнопорождённых абелевых групп, их также можно использовать для построения p -адических чисел.
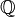— кольцо рациональных чисел, являющееся полем. Это простейшее поле характеристики 0. Оно является основным объектом исследования в теории чисел. Пополнение его по различным неэквивалентным нормам даёт поля вещественных чисел 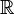и p -адических чисел 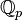, где p — произвольное простое число.
Для произвольного коммутативного кольца 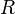можно построить кольцо многочленов от n переменных 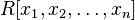с коэффициентами в 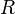. В частности, 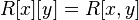. Кольцо многочленов с целыми коэффициентами является универсальным кольцом многочленов, в том смысле что все кольца многочленов выражаются через тензорное произведение: .
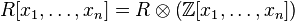Кольцо бесконечно гладких вещественнозначных функций 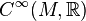на многообразии 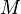— это коммутативное кольцо с единицей. Умножение и сложение в нём определяются поточечно:

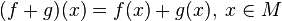
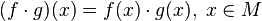
Нулевой элемент — функция, тождественно равная 0, единичный — тождественно равная 1. Обратимыми элементами в нём являются нигде не равные 0 функции, делителями нуля — функции, равные 0 на некотором открытом множестве в 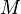. Это кольцо не имеет нильпотентов, так как их нет в 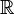, а умножение поточечно. Если 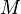компактно, то максимальными идеалами в нём являются множества функций, зануляющихся в данной точке:

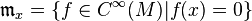
причём максимальные идеалы совпадают с простыми.

Кольцо подмножеств множества 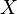— это кольцо, элементами которого являются подмножества в 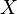. Операция сложения есть симметрическая разность, а умножение — пересечение множеств:

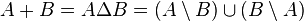
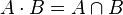
Аксиомы кольца легко проверяются. Нулевым элементом является пустое множество, единичным — всё 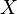. Все элементы кольца являются идемпотентами, то есть 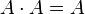. Любой элемент является своим обратным по сложению: 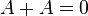. Кольцо подмножеств важно в теории булевых алгебр и теории меры, в частности в построении теории вероятностей.

Кольцо когомологий — это важный топологический инвариант, связанный с любым топологическим пространством.
Если 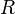— кольцо в категории 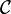, то множество 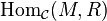является кольцом (в обычном смысле) для любого объекта .
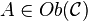Кольцо периодов — множество чисел, которые могут быть выражены как объём области в 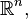заданной системой полиномиальных неравенств с рациональными коэффициентами.

РАДИКАЛ КОЛЬЦА

Правило 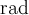, сопоставляющее каждому кольцу 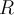некоторый идеал 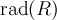, такой что

;
;
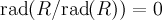для любого гомоморфизма колец 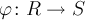имеет место включение ,

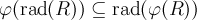называется радикалом ¹⁾ кольца.

Для кольца 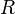идеалом называется подкольцо, замкнутое относительно умножения на элементы из 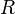. При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из 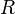. Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.

Более точно: Идеалом кольца 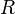называется такое подкольцо 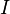кольца 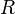, что

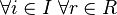произведение 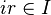(условие на правые идеалы);
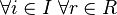произведение 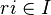(условие на левые идеалы).

Аналогично для полугруппы её идеалом называется подполугруппа, для которой верно какое-нибудь из этих условий (или оба для двустороннего идеала), то же самое и для алгебры.

РАДИКАЛ ИДЕАЛА

Радикал идеала I — это множество 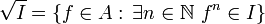. Оно тоже является идеалом кольца A, если только кольцо A коммутативно. В случае, когда I=(0), этот идеал называется нильрадикалом кольца A. Его элементами являются все нильпотентные элементы кольца. Если коммутативное кольцо не имеет нильпотентных элементов, кроме нуля, (имеет нулевой нильрадикал), — оно называется радикальным. Идеал I называется радикальным, если он совпадает со своим радикалом. В этом случае факторкольцо R/I не имеет нильпотентных элементов, кроме нуля.

ПОЛЕ

По́лем называется множество F с двумя бинарными операциями 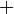(аддитивная операция или сложение) и (мультипликативная операция или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей, все ненулевые элементы которого обратимы.

Иными словами, множество F с двумя бинарными операциями 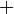(сложение) и (умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.

Характеристика поля всегда 0 или простое число.

Поле характеристики 0 содержит 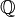, поле рациональных чисел.
Поле характеристики p содержит 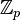, поле вычетов по модулю .

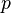Количество элементов в конечном поле всегда равно 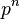, степени простого числа.

При этом для любого числа вида 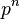существует единственное (с точностью до изоморфизма) поле из 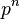элементов, обычно обозначаемое .

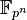Любой гомоморфизм полей является вложением.

Примеры

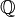— рациональные числа,

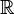— вещественные числа,

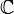— комплексные числа,

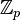— поле вычетов по модулю p, где p — простое число.

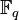— конечное поле из 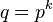элементов, где p — простое число, k — натуральное.

Дистрибути́вность (от латинского distributivus — «распределительный») — свойство согласованности двух бинарных операций, определённых на одном и том же множестве.

Говорят, что две бинарные операции + и × удовлетворяют свойству дистрибутивности, если для любых трех элементов :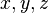

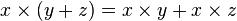— дистрибутивность слева;

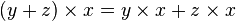— дистрибутивность справа.

АЛГЕБРА

Алгебра (универсальная алгебра) — множество 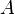, называемое носителем алгебры, снабжённое набором 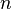-арных алгебраических операций на 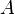, называемым сигнатурой, или структурой алгебры. Иными словами, универсальной алгеброй является алгебраическая система с пустым множеством отношений.

Свойства

Для универсальных алгебр имеет место теорема о гомоморфизме: если 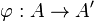— гомоморфизм алгебр, а 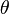— ядерная конгруэнция 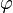(то есть 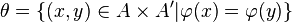, то факторалгебра 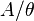изоморфна .

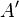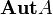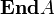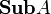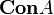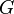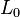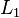Для универсальных алгебр исследованы сопутствующие структуры: группа автоморфизмов , моноид эндоморфизмов , решётка подалгебр , решётка конгруэнций , в частности, показано, что для любой группы и решёток и существует такая универсальная алгебра 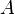, что , , .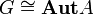

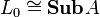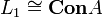Универсальная алгебра с одной бинарной алгебраической операцией называется группоидом (магмой).

КОЛЬЦО МНОГОЧЛЕНОВ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Определение

Многочлен от n переменных X ₁,…, X_n с коэффициентами в поле K определяется аналогично многочлену от одной переменной, но обозначения становятся более сложными. Для любого мультииндекса α = (α ₁,…, α_n), где каждое α_i — ненулевое целое число, пусть

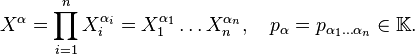
X^α называется одночленом степени 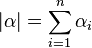. Многочлен — это конечная линейная комбинация одночленов с коэффициентами в K: .

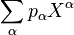Многочлены от n переменных с коэффициентами в поле k (с обычными операциями сложения и умножения) образуют коммутативное кольцо, обозначаемое k [ x ₁,…, x_n ]. Это кольцо можно получить многократным применением операции «взятие кольца многочленов над данным кольцом». Например, k [ x ₁, x ₂] изоморфно k [ x ₁][ x ₂], как и k [ x ₂][ x ₁]. Это кольцо игрет фундаментальную роль в алгебраической геометрии. Многие результаты коммутативной алгебры были достигнуты благодаря изучению идеалов этого кольца и модулей над ним.