Теорема про змiну кiлькостi руху матерiальної системи

 

Похiдна за часом вiд вектора кiлькостi руху системи матерiальних точок дорiвнює головному вектору всiх зовнiшнiх сил, дiючих на систему:

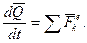                           (13.6)

Кiлькiстю руху матерiальної системи називається вектор 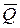, рiвний сумi кiлькостей руху матерiальних точок, що входять в систему:

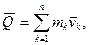                            (13.7)

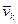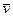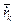де m_k - маса k -тої матерiальної точки, - її швидкiсть. Через те, що _k = , де 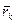– радiус-вектор k -тої точки, проведений з початку iнерцiальної системи вiдлiку, то з (13.7) маємо:

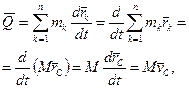             (13.8)

де 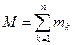- маса матерiальної системи,  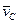– швидкiсть центра мас. З формули (13.8) зробимо висновок: кiлькiсть руху матерiальної системи дорівнює добутку маси всiєї системи та швидкості її центра мас. В проекцiях на нерухомi осi декартових координат векторне рiвняння (13.6) еквiвалентне трьом скалярним:

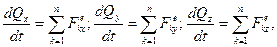(13.9)

де

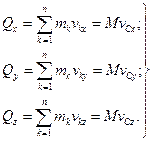                 (13.10)

Ця теорема має декiлька наслiдкiв:

а) внутрiшнi сили безпосередньо не впливають на змiну кiлькостi руху матерiальної системи – вони можуть впливати на рух через зовнiшнi сили;

б) якщо головний вектор всiх зовнiшнiх сил, дiючих на систему, дорiвнює нулю, то вектор кiлькостi руху матерiальної системи залишається постiйним за величиною i напрямком:

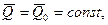
де 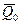– початкове значення вектора ;

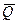в) якщо проекцiя головного вектора всiх зовнiшнiх сил, прикладених до системи, на будь-яку нерухому вiсь дорiвнює нулю, то проекцiя кiлькостi руху матерiальної системи на цю вісь залишається постiйною:

Q_x = Q _{0 x} = const,

де Q _{0 x} - початкове значення проекцiї Q_x.

Рiвнiсть (13.6) можна записати i так:

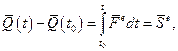            (13.11)

де 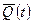– кiлькiсть руху матерiальної системи в момент часу t, 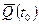- кiлькiсть руху матерiальної системи в момент часу t ₀,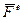 – головний вектор зовнiшнiх сил, 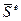 = Σ 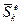– головний вектор iмпульсiв зовнiшнiх сил.

Рiвнiсть (13.11) виражає теорему про змiну кiлькостi руху матерiальної системи в iнтегральнiй формi:

змiна кiлькостi руху матерiальної системи за промiжок часу [ t ₀, t ] дорiвнює головному вектору iмпульсiв всiх зовнiшнiх сил, прикладених до системи, за той же промiжок часу.

Векторне рiвняння (13.11) еквiвалентне трьом скалярним рiвнянням:

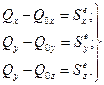                         (13.12)

де S_x^e, S_y^e i S_z^e - проекцiї головного вектора iмпульсiв всiх зовнiшнiх сил на осi координат; Q_x, Q_y, Q_z i Q _{0 x} , Q _{0 y} , Q _{0 z} – значення проекцiй кiлькостi руху матерiальної системи в моменти часу t i t ₀ відповідно.

Теорему про змiну кiлькостi руху матерiальної системи в формi (13.11) або (13.12) широко застосовують в теорiї удару.

При розв’язаннi задач за допомогою теореми про змiну кiлькостi руху матерiальної системи корисно дотримуватись такого порядку:

1) показати на рисунку всi зовнiшнi сили;

2) вибрати систему координат;

3) записати теорему про змiну головного вектора кiлькостi руху в проекцiях на осi координат;

4) з одержаних рiвнянь визначити шуканi величини.

 

Теорема Ейлера

 

Сума головних векторiв об’ємних i поверхневих сил, а також векторiв секундних кiлькостей руху рiдини, яка протiкає через два перерiзи труби, дорiвнює нулю, якщо вектори секундних кiлькостей руху направленi у середину видiленого перерiзами об’єму:

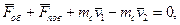            (13.13)

де m_c = ρ ₁ v ₁ S ₁ = ρ ₂ v ₂ S ₂ - секундна маса - маса рiдини, що протiкає за одиницю часу через перерiз площею S ₁ або S ₂;

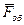-головний вектор об’ємних сил. Об’ємними називаються сили, якi дiють на всi частинки рiдини, розташованi як у серединi, так i на поверхнi розглянутого об’єму (наприклад, сили ваги частинок рiдини);

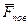-головний вектор поверхневих сил. Поверхневими силами називаються сили, якi дiють на частинки рiдини, розташованi на зовнiшнiй поверхнi об’єма (наприклад, реакцiї стiнок труби);

ρ - густина рiдини.

При користуваннi теоремою Ейлера потрiбно:

1) показати на рисунку об’ємнi i поверхневi сили;

2) показати на рисунку вектори секундних кiлькостей руху рiдини (або газу), протiкаючої через два перерiзи, що обмежують розглядуваний об’єм рідини, при цьому вектори секундних кiлькостей руху треба направити всередину цього об’єму;

3) вибрати систему координат;

4) записати теорему Ейлера в проекцiях на осi декартових координат:

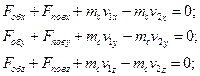        (13.14)

5) визначити шуканi величини.

 

Рiвняння Мещерського

 

Розглянемо матерiальну систему, обмежену поверхнею S. Маса в поверхнi S змiнюється за заданим законом m = m (t), тобто задана функцiєю часу (рис. 13.1).

Рис. 13. 1.

 Запишемо теорему про змiну кiлькостi руху системи:

                      

 

 

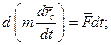
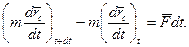              (13.15)

Позначимо абсолютну швидкість центра мас всередині поверхні S в момент 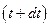через 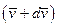. Нехай 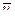– абсолютна швидкість викинутих частинок з масою 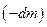. В цих позначеннях рівняння (13.12) перепишемо так:

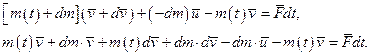
Нехтуючи величиною dm×d 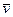, одержимо:

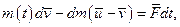
звiдси

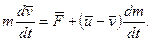                   (13.16)

Величина 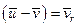 є по вiдношенню до рухомої точки вiдносною швидкiстю викинутих частинок. Тодi

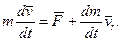                       (13.17)

Величина

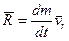
називається реактивною силою.

Рiвняння (13.17) називають рiвнянням Мещерського.

Якщо вiдносна швидкiсть 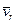 = 0, то  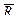= 0 i рiвняння (13.17) приймає вигляд:

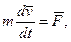
це другий закон Ньютона.

Якщо абсолютна швидкiсть викинутих частинок 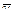 = 0, то з (13.16) одержимо:

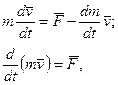
що по формi також спiвпадає з другим законом Ньютона.

13. 5. Задачi Цiолковського.

 

Перша задача. Визначити швидкiсть v руху ракети, якщо вiдносна швидкiсть v_r витiкання газiв постiйна за модулем i направлена в бік, протилежний руховi ракети. Ракета з безперервним витiканням газiв летить вертикально вгору. Опором повiтря i силою ваги нехтуємо.

Розглядаємо ракету як точку змiнної маси i запишемо рiвняння Мещерського для випадку :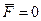

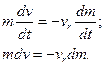
Роздiлимо змiннi

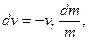
проiнтегруємо

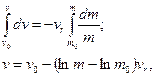
де v ₀- початкова швидкiсть ракети; m ₀- початкова маса ракети.

Значить

v = v ₀ + v_r ln(m ₀ /m).                        (13.18)

Ця формула називається формулою Цiолковського. Нею можна користуватися для наближеного обчислення швидкостi ракети в тих випадках, коли сила опору i сила ваги не є великими порiвняно з реактивною силою.

Розв’яжемо таку задачу. Яким повинно бути вiдношення початкової маси ракети до маси в кiнцi горіння пального для досягнення ракетою першої космiчної швидкостi, якщо вiдносна швидкiсть викидання частинок постiйна i дорiвнює 3000 м/с?

Дано: v = 7910 м/с; v ₀ = 0; v_r = 3000 м/с.

Знайти: m ₀ /m.

Розв’язання. По формулi Цiолковського маємо:

7910 = 3000ln(m ₀ /m);   ln(m ₀ /m) = (7910/3000) = 2,64;

(m ₀ /m) = e ^2,64; (m ₀ /m) = 14,0.

Значить, m ₀ = 14,0 m: стартова вага ракети повинна бути в 14 разiв бiльша за вагу останнього ступеня ракети.

Друга задача. Ракета рухається в однорiдному полi сил ваги вертикально вгору з постiйним прискоренням а. Ефективна швидкiсть витiкання газiв v_r постiйна. Визначити: 1) закон змiни маси ракети; 2) час Т, за який маса ракети зменшиться в 2 рази.

Розглянемо рух ракети, запущеної з поверхнi Землi в системi координат з початком в точцi запуску (рис. 13.2).

Рiвняння Мещерського запишемо так:

Рис. 13. 2.

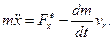
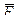Сила  представляє собою результуючу складання сили притягання i сили аеродинамiчного опору

 

атмосфери. Реактивна сила

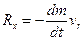
направлена в бiк додатного напряму осi х, бо (dm/dt) < 0. Введемо позначення: S - площа вихiдного перерiзу сопла; Р - тиск в газовому потоцi на зрiзi сопла; р (х) - статичний атмосферний тиск.

Сила, обумовлена тиском газового потоку i статичним тиском атмосфери, дорiвнює (Р- р (х)).

Тоді сила тяги двигуна ракети

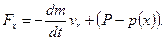
При русi в пустотi   р (х) = 0  i

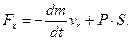
Це спiввiдношення запишемо так:

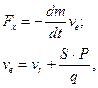
де

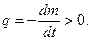
Величина v_e>v_r називається ефективною швидкiстю витiкання.

Таким чином, рух ракети описується рiвнянням:

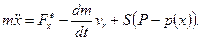         (13.19)

Розв’язок цього рiвняння є складним. При вiдсутностi атмосфери з (13.19) одержимо:

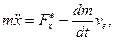                       (13.20)

де 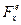  - сила тяжiння.

Якщо знехтувати силою тяжiння i силою опору атмосфери, то з (13.20) маємо:

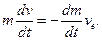
Звідси

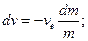
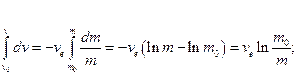
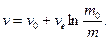                      (13.21)

Позначимо z = (m ₀ /m) - це число Цiолковського.

У випадку нашої задачi рiвняння (13.20) записуємо так:

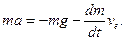
Роздiлимо змiннi

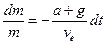
та проінтегруємо

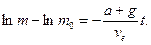
Звiдси

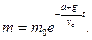
При m = m ₀ / 2,   t = T:

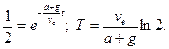
Якщо ракета рухається при g = 0 (полe тяжiння вiдсутнє), то

 

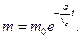
Зауваження. Для закріплення матеріалу §13 (пункти 13.2 – 13.5) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 36.1 - 36.6, 45.2, 45.4;

2) № 36.7 - 36.9, 36.11 - 36.13, 45.8 - 45.12, 45.16, 45.18 – 45.20, 45.27;

3) № 36.10, 36.14, 45.22 – 45.24, 45.26, 45.28, 45.29, 45.34.

Рекомендується розв’язати також задачі № 9.4, 9.5, 17.2 - 17.8 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.