Непрерывность функции в точке

       Функция 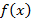 называется непрерывной в точке , если существует конечный предел равный значению этой функции в этой точке

Если нарушено требование непрерывности, тогда функция имеет разрыв. Разрывы могут быть двух видов: разрывы с различным левым и правым пределом и разрывы, предел в которых равен бесконечности.

       Если 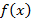 определена в проколотой окрестности точки , но не определена в самой точке  или 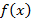 определена в окрестности , но не является непрерывной в точке , тогда точка  называется точкой разрыва функции .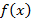

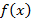       Пусть  – точка разрыва для , тогда если существуют конечные левый и правый пределы данной функции, тогда такой разрыв – разрыв первого рода. Пример разрыва первого рода представлен на рисунке 40.

Рисунок 40. Разрыв первого рода.

Если не выполняется условие разрыва первого рода, тогда такой разрыв – разрыв второго рода. Пример разрыва второго рода представлен на рисунке 41.

Рисунок 41. Разрыв второго рода.

Все элементарные функции непрерывны во всех точках своей области определения.

Теорема: Если 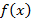 и  непрерывны в точке , тогда их сумма, разность, произведение и отношение также непрерывны в этой точке. Композиция непрерывных функций также непрерывна.