Функция называется непрерывной на интервале  , если она непрерывна в каждой точке этого интервала.
, если она непрерывна в каждой точке этого интервала.
Функция называется непрерывной на отрезке 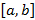 , если она непрерывна в каждой точке этого интервала
, если она непрерывна в каждой точке этого интервала  и на концах этого отрезка, то есть существуют конечные левые и правые пределы на соответствующих концах отрезка.
и на концах этого отрезка, то есть существуют конечные левые и правые пределы на соответствующих концах отрезка.
Свойства функция непрерывных на отрезке:
1. Если функция 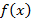 непрерывна на отрезке
непрерывна на отрезке 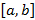 , тогда она ограничена. Непрерывность на интервале не гарантирует ограниченности;
, тогда она ограничена. Непрерывность на интервале не гарантирует ограниченности;
2. Если функция 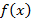 непрерывна на отрезке
непрерывна на отрезке 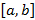 , тогда она достигает своего наибольшего M и наименьшего значения m. Иными словами, можно указать точки
, тогда она достигает своего наибольшего M и наименьшего значения m. Иными словами, можно указать точки 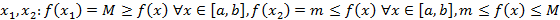 ; Непрерывность на интервале не гарантирует ни наличие M и m, ни их достижения.
; Непрерывность на интервале не гарантирует ни наличие M и m, ни их достижения.
3. Если 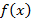 непрерывна на отрезке
непрерывна на отрезке 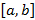 и m и M – неменьшее и наибольшее значение функции на заданном отрезке, тогда любое промежуточное значение
и m и M – неменьшее и наибольшее значение функции на заданном отрезке, тогда любое промежуточное значение 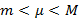 обязательно принимает в некоторой точке
обязательно принимает в некоторой точке 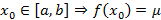 . Если непрерывности на отрезке нет, тогда некоторые промежуточные значения могут не приниматься такой функцией;
. Если непрерывности на отрезке нет, тогда некоторые промежуточные значения могут не приниматься такой функцией;
4. Если 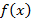 непрерывна на отрезке
непрерывна на отрезке 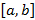 и значения на концах
и значения на концах 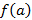 и
и 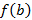 имеют разные знаки, тогда существует точка
имеют разные знаки, тогда существует точка 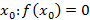 .
.
Сравнение БМФ и ББФ
Пусть 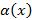 и
и  – БМФ при
– БМФ при 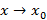 или
или 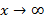 , тогда при
, тогда при 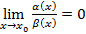 функция
функция 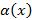 – БМФ более высокого порядка, чем
– БМФ более высокого порядка, чем 
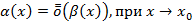
Если 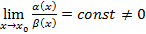 , тогда
, тогда 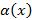 и
и  – БМФ одного порядка малости
– БМФ одного порядка малости
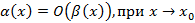
Частный случай при 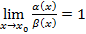 , тогда
, тогда 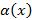 и
и  называют эквивалентными при
называют эквивалентными при 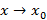
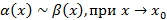
Теорема: В случае неопределенности  весь числитель и весь знаменатель можно заменить на эквивалентные функции
весь числитель и весь знаменатель можно заменить на эквивалентные функции
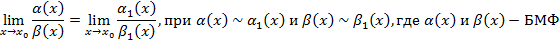
Если числитель и знаменатель представлены произведением функций, тогда множитель также можно заменить на эквивалентный. Нельзя менять на эквивалентные в случае суммы.
Пусть 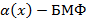 при
при 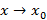 , тогда справедливы следующие соотношения
, тогда справедливы следующие соотношения

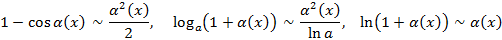
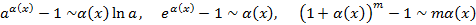
Аналогично анализируются ББФ, для которых также справедливы указанные соотношения.
Производная
Пусть задана непрерывная в точке  функция
функция 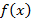 . Рассмотрим приращение аргумента
. Рассмотрим приращение аргумента 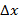 , тогда получим приращение функции в точке
, тогда получим приращение функции в точке 
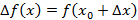 . Приращение аргумента может быть как больше нуля, так и меньше, что задает правое и левое движение по указанной функции. В связи с этим приращение функции также может быть больше или меньше нуля.
. Приращение аргумента может быть как больше нуля, так и меньше, что задает правое и левое движение по указанной функции. В связи с этим приращение функции также может быть больше или меньше нуля.
Знаки приращения функции и приращения аргумента будут совпадать для возрастающих функций или будут противоположными при убывающих функций.
Предел отношения приращения функции к приращению аргумента при  называется производной функции
называется производной функции

Производная в некоторой точке  – число. Если рассматривать производную в произвольной точке, тогда
– число. Если рассматривать производную в произвольной точке, тогда 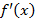 – функция.
– функция.
Производные некоторых элементарных функций
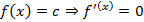 ,
, 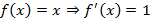 ,
, 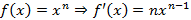
 ,
, 
 ,
,  ,
,
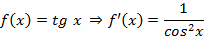
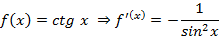
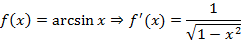
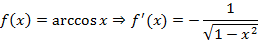
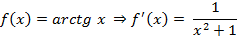
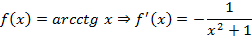
В физическом смысле производная позволяет найти мгновенную скорость тела в заданный момент времени используя функцию расстояния.
Пусть найдена производная некоторой функции и равна 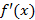 , поскольку это также функция, тогда для нее тоже можно искать производную. Производная любого порядка примет вид
, поскольку это также функция, тогда для нее тоже можно искать производную. Производная любого порядка примет вид
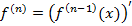
 2020-08-05
2020-08-05 132
132








