2020-08-05
176
Пусть дана некоторая кривая и фиксированная точка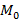 
на ней. Выберем произвольную точку 
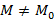на этой же кривой и проведем секущую. Пусть 
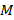движется по кривой к 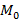, тогда секущая 
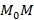меняет свое положение. Если в момент слияния 
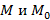секущая занимает однозначное положение, тогда это предельное положение секущей, которая называется касательной. Все вышеуказанные построения представлены на рисунке 42.
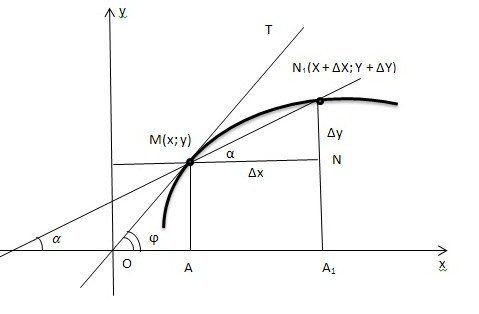
Рисунок 42. Построение касательной к графику функции.
Касательная существует не всегда. Например, на рисунке 43 показано, что у некоторого графика функции при выборе точки, предельное положение секущей различны.
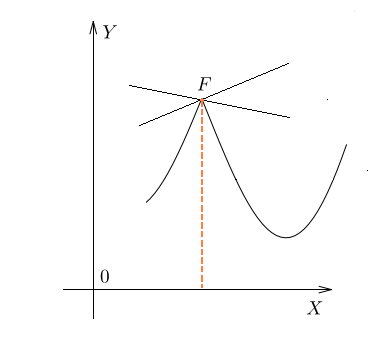
Рисунок 43. Пример функции, когда касательная не существует в точке F.
Рассмотрим график функции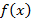 
, на котором зафиксирована точка 
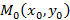на графике и выбрана произвольная 
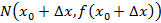, как указано на рисунке 42. Обозначим 
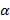– угол наклона секущей; 
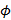– угол наклона касательной
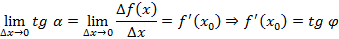
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функций в этой точке – геометрический смысл производной.
Уравнение касательной примет вид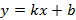 
, поскольку касательная проходит через точку 
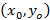, где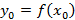 
, тогда уравнение касательной примет вид
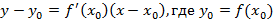
Нормалью к графику функции в точке 
называется прямая перпендикулярная касательной, построенной в этой же точке. Пример нормали к графику функции представлен на рисунке 44.
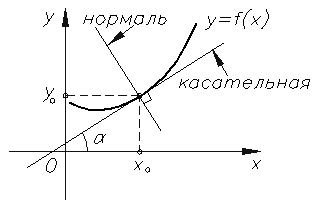
Рисунок 44. Нормаль относительно касательной к графику функции.
Уравнение нормали, учитывая ее расположение относительно касательной, примет вид
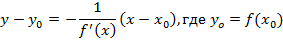
Дифференциал
Пусть функция 
имеет в точке производную, тогда приращение дифференцируемой функции примет вид
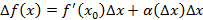
Приращение дифференцируемой функции состоит из двух частей: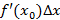 
– пропорциональна приращению аргумента и 
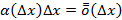– малая по сравнению с приращением аргумента – первая главная линейная часть приращения.
Главная линейная часть приращения называется дифференциалом
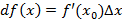
Геометрический смысл дифференциала – приращение касательной к функции. Обозначение производной функции – отношение дифференциалов функции и переменной
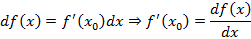
При фиксированной точке дифференциал зависит только от приращения аргумента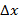 
, изменение которого меняет дифференциал.
Правила дифференцирования
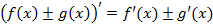
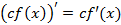
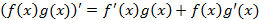
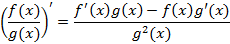
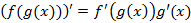
Теорема Лопиталя: Пусть и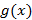 
непрерывные и дифференцируемые функции в окрестности точки , причем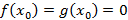 
, тогда
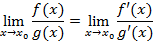
может быть конечным чистом и может быть бесконечностью и данное соотношение справедливо для неопределенностей 
и 
.
