Функция монотонно возрастает, если ее производная в некоторой точке больше нуля, иначе если функция монотонно убывает, тогда ее производная в некоторой точке меньше нуля. Промежуток, на котором знак производной постоянен – промежуток монотонности функции. Такие промежутки разделяются точками, где производная равна нулю или не существует – критическими точками первой производной.
Точка  называется локальным максимумом функции
называется локальным максимумом функции 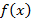 , если
, если 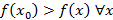 из некоторой окрестности точки
из некоторой окрестности точки  . Аналогично определяется локальный минимум:
. Аналогично определяется локальный минимум:
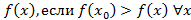 окрестности точки
окрестности точки  . Точки локальных максимумов и минимумов называются локальными экстремумами.
. Точки локальных максимумов и минимумов называются локальными экстремумами.
Смена характера монотонности в точке 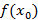 означает наличие в этой точке экстремума для
означает наличие в этой точке экстремума для  , что показывает на критическую точку для
, что показывает на критическую точку для 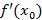 .
.
Из свойств непрерывных на отрезке функций знаем, что они достигают своего наибольшего и наименьшего значения на отрезке 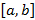 . Эти значения достигаются в точках локальных экстремумов или на концах отрезком.
. Эти значения достигаются в точках локальных экстремумов или на концах отрезком.
Исследование функции с помощью второй производной
Пусть у функции  в точке
в точке  существует невертикальная касательная, тогда, если график функции в некоторой окрестности точки
существует невертикальная касательная, тогда, если график функции в некоторой окрестности точки  расположен под касательной, тогда
расположен под касательной, тогда  – точка выпуклости, иначе – над касательной, тогда
– точка выпуклости, иначе – над касательной, тогда  – точка вогнутости. В обоих случаях график находится по одну сторону от касательной.
– точка вогнутости. В обоих случаях график находится по одну сторону от касательной.
Если на промежутке 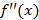 сохраняет постоянный знак, тогда сама функция
сохраняет постоянный знак, тогда сама функция  имеет постоянный характер выпуклости на этом промежутке. Эти промежутки отделяются друг от друга точками, где
имеет постоянный характер выпуклости на этом промежутке. Эти промежутки отделяются друг от друга точками, где 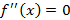 или не существует. Такие точки называются критическими точками второй производной.
или не существует. Такие точки называются критическими точками второй производной.
Пусть у функции  в точке
в точке  существует касательная, возможно вертикальная, и при переходе через эту точку характер выпуклости меняется, тогда
существует касательная, возможно вертикальная, и при переходе через эту точку характер выпуклости меняется, тогда  называется точкой перегиба.
называется точкой перегиба.
Асимптоты
Асимптотой называется прямая, к которой неограниченно приближается уходящая в бесконечность весть графика. Асимптоты могут быть трех видов: горизонтальные, вертикальные и наклонные.
Горизонтальные асимптоты возникают, когда существует предел 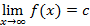 . В этом случае уравнение асимптоты примет вид
. В этом случае уравнение асимптоты примет вид 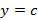 . Пример горизонтальных асимптот графика
. Пример горизонтальных асимптот графика 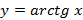 представлен на рисунке 46.
представлен на рисунке 46.
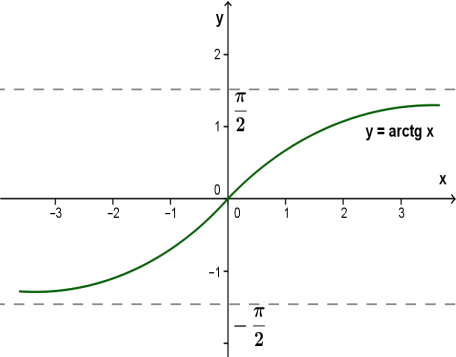
Рисунок 46. График функции с горизонтальными асимптотами.
Вертикальные асимптоты возникают, когда существует конечная точка  , в которой
, в которой 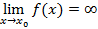 . Пример вертикальных асимптот графика
. Пример вертикальных асимптот графика 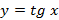 представлен на рисунке 47.
представлен на рисунке 47.
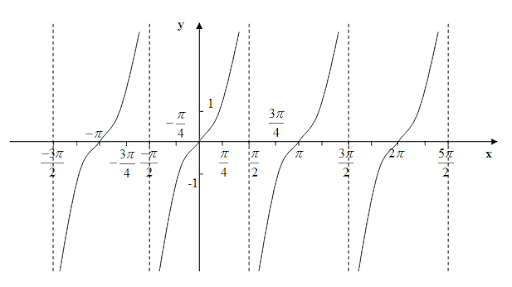
Рисунок 47. График функции с вертикальными асимптотами.
Наклонные асимптоты возникают, когда существуют конечные пределы такого вида
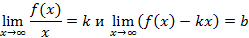
В этом случае асимптотой будет прямая 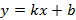 . Пример наклонных асимптот графика
. Пример наклонных асимптот графика 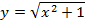 представлен на рисунке 48.
представлен на рисунке 48.
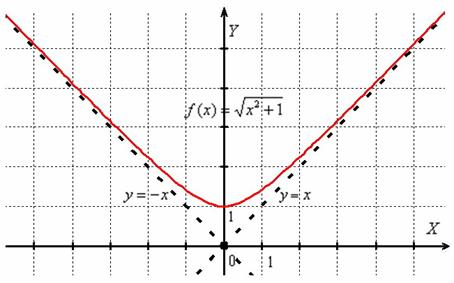
Рисунок 48. График функции с наклонными асимптотами.
 2020-08-05
2020-08-05 201
201








