Если среди чисел k и m хотя бы одно нечетное вида  , тогда интеграл тригонометрической функции преобразуется по следующему соотношению
, тогда интеграл тригонометрической функции преобразуется по следующему соотношению
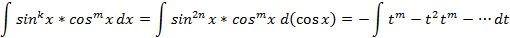
Данное соотношение получено путем внесения множителя под дифференциал и следующей заменой  . Если в данном интеграле все степени четные, тогда можно воспользоваться формулами понижения степени.
. Если в данном интеграле все степени четные, тогда можно воспользоваться формулами понижения степени.
Рациональной функцией двух переменных  называется отношение двух многочленов от двух переменных
называется отношение двух многочленов от двух переменных  . Многочленом двух переменных называется сумма одночленов вида
. Многочленом двух переменных называется сумма одночленов вида 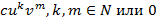 . Если в рациональную функцию подставить
. Если в рациональную функцию подставить
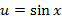 и
и 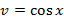 , тогда получим рациональную функцию относительно
, тогда получим рациональную функцию относительно 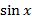 и
и  -
- 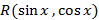 .
.
Интеграл вида 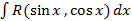 всегда рационализируется заменой
всегда рационализируется заменой 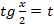 – универсальная подстановка
– универсальная подстановка
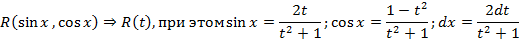
Из данных соотношений следуют возможные частные подстановки следующих видов
1. 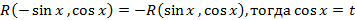 ;
;
2.  ;
;
3. 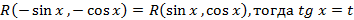 .
.
 2020-08-05
2020-08-05 88
88








