Определенный интеграл

Назовем определенным интегралом на отрезке 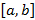от функции число равное приращению первообразной на этом отрезке

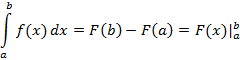
Данное соотношение – формула Ньютона-Лейбница. Функция должна быть непрерывна.

Если 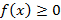на отрезке 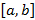, тогда определенный интеграл этой функции равен площади криволинейной трапеции – фигуры, ограниченной графиком функции и отрезком 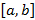– геометрический смысл определенного интеграла, пример приведен на рисунке 49.

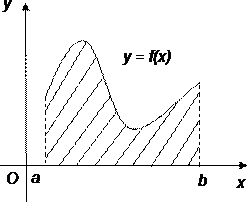
Рисунок 49. Геометрический смысл определенного интеграла.

Свойства определенного интеграла:

1. ;

2. ;

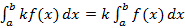3. ;

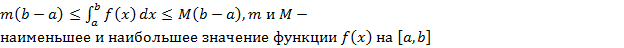
5. .

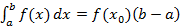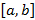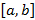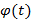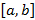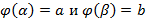Пусть непрерывна на a непрерывно-дифференцируемая на , причем значения на этом отрезке не выходят за пределы и , тогда

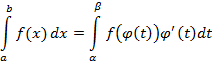
Данное соотношение определяет способ замены переменной в определенном интеграле.

Пусть 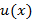и непрерывно-дифференцируемые функции, тогда

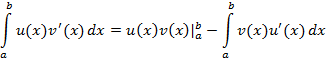
Данное соотношение определяет интегрирование по частям для определенного интеграла.

Определенный интеграл имеет следующие приложения

1. Определение площади криволинейной трапеции

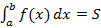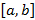Если , тогда . В случае знакопременности функции на отрезке , тогда 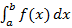– алгебраическая сумма площадей криволинейных трапеций, разделенных нулями, заданными функции (пример указан на рисунке 50).

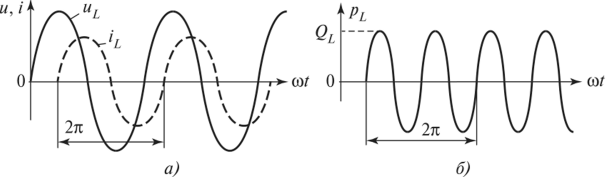
Рисунок 50. Знакопеременная функция сигнала.

2. Вычисление длины кривой

Пусть непрерывно-дифференцируемая функция, тогда длина графика l на отрезке 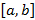равна соотношению

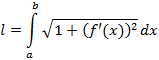
3. Вычисление объемов тел вращения

Пусть 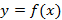непрерывна на отрезке 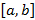. При вращении криволинейной трапеции относительно оси Ox охватывается некоторая область пространства, которая называется телом вращения. Аналогично, если монотонная функция, тогда можно рассмотреть тело вращения относительно оси Oy. Объемы тел вращения могут быть найдены по следующим формулам