Первообразная и неопределенный интеграл

       Если 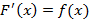, тогда  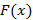называется первообразной для . Исходя из свойств дифференцирования 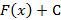 также будет первообразной для 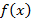, поскольку

Если 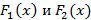 – первообразные для , тогда справедливо следующие соотношение

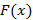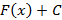Если  – первообразная для , тогда семейство , где C – произвольная константа, описывает все первообразные. Семейство первообразных функции  называют ее неопределенным интегралом

Неопределенный интеграл обладает следующими свойствами:

1. ;

2. ;

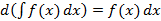3. ;

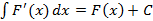4. ;

5. ;

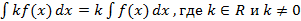6. ;

Некоторые основные соотношения неопределенных интегралов:

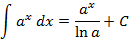
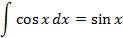
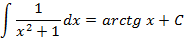
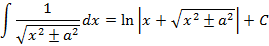
Данные соотношения можно проверить дифференцированием правой части.

 

Замена переменной в определенном интеграле

       Пусть  непрерывная функция, 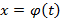 – непрерывно-дифференцируемая функция, тогда справедливо соотношение, которое можно получить формальной заменой  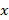на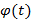

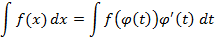
Замена переменной чаще производится справа на лево следующим образом

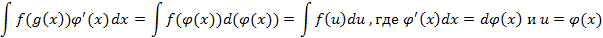
 – вынесение из дифференциала;

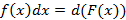 – поднесение под дифференциал;

       Интегралы вида 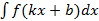 можно вычислять двумя способами

В данном случае происходят следующие замены: , из которых вытекает соотношение: .

       Второй способ подразумевает использование соотношения .

Интегрирование по частям

       Пусть 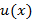 и  – непрерывно-дифференцируемые функции, тогда справедливо следующие соотношение

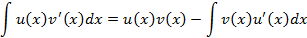
Данное соотношение можно упростить, если произвести две замены следующего вида  и , тогда получим

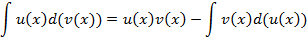
       Основные виды интегралов, берущихся по частям имеют вид

В данных соотношениях P(x) и Q(x) - некоторые многочлены.

 

Рациональные функции

       Функция, представленная как отношение двух многочленов называется рациональной функцией R(x)

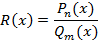
Рациональная функция называется правильной, если 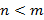 или неправильной, если .

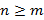       Любую неправильную рациональную дробь можно разложить в сумму многочлена и правильной рациональной дроби. Такой прием можно использовать при интегрировании рациональных функций.

       Элементарные рациональные дроби – правильные рациональные функции следующих четырех типов

Интегрирование элементарных дробей первых трех типов соответственно имеет вид

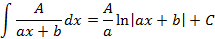
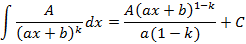
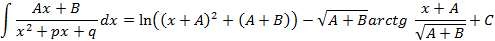
Теорема: Любой многочлен можно представить как произведение скобок вида 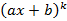 и .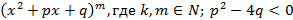

       Любую правильную рациональную дробь можно разложить в в сумму элементарных дробей по следующему алгоритму

1. Готовим знаменатель по указанной выше теореме;

2. Каждой скобке знаменатель ставим в соответствие в группу элементарных по следующим правилам

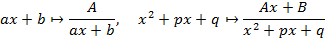
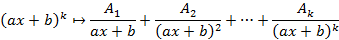
Коэффициенты A и B находятся методом неопределенных значений или методом произвольных значений. Метод неопределенных значений подразумевает приравнивание числительных при одинаковых знаменателях, после чего производится подбор коэффициентов. Метод произвольных значений подразумевает подстановку x в обе части получаемого уравнения и подбор коэффициентов.