2020-08-05
106
Для функции двух переменных существование конечных частных производных не гарантирует не только гладкость, но и непрерывность. Если непрерывная функция
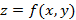в точке 
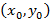имеет полное приращение 
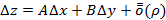, где
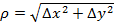, тогда функцию называют дифференцируемой в точке 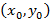. Если 
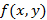– дифференцируема, тогда справедливо следующее соотношение
Дифференцируемость геометрически означает гладкость графика функции двух переменных, из чего следует, что к данному графику можно провести касательную плоскость. У дифференцируемой функции двух переменных в точке 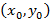существует касательная плоскость и ее уравнение привет вид
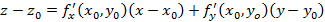
Пример касательной плоскости к функции двух переменных представлен на рисунке 57.
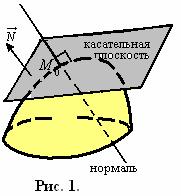
Рисунок 57. Касательная плоскость.
Производная по направлению
Пусть 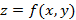– дифференцируемая функция, 
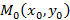– некоторая точка в области определения данной функции, 
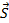– вектор в плоскости xOy. Рассмотрим приращение 
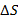в точке 
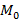в направлении вектора 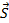, тогда из 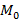попадаем в точку
|
|
|
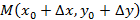. Возьмем полное приращение
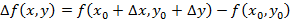и рассмотрим 
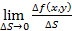, если этот предел существует и конечен, тогда он называется производной по направлению S функции 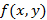в точке .
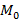Геометрически производная по направлению характеризует скорость изменения функции 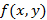в направлении 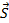в точке .
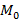Для дифференцируемой функции 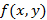в точке 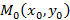производную по направлению 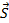можно найти, исходя из соотношения
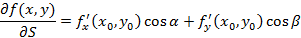
В данном соотношении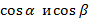 
– направляющие косинусы для вектора .
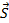Градиент
Градиентом функции двух переменных называется вектор, координаты которого составлены из частных производных рассматриваемой функции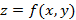
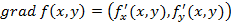
Если в каждой точке области определения функции построить вектор градиента, тогда получим векторное поле градиентов.
Свойства градиента:
1. В каждой точке вектор градиента задает направление, в котором функция растет быстрее всего;
2. Вектор, противоположный градиенту, указывает направление, в котором функция убывает быстрее всего;
3. Если взять в точке прямую, перпендикулярную градиенту, тогда она будет касательной к линии уровня, проходящей через точку.
