2020-08-05
91
Частные производные функции двух переменных по x и y также являются функциями двух переменных, поэтому для них можно брать частные производные
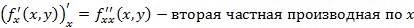
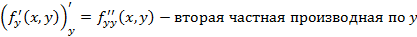
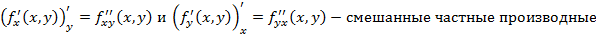
Если у функции двух переменных существуют непрерывные частные и смешанные производные, тогда смешанные частные производные равны.
Аналогично можно строить частные производные более высоких порядков. Для них также справедливо утверждение о независимости частной производной от порядка, в котором идет дифференцирование, если все промежуточные частные производные и результат непрерывны.
Локальные экстремумы для функции двух переменных
Точка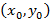 
называется локальным максимумом функции двух переменных 
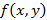, если справедливо следующие соотношение в некоторой окрестности заданной точки
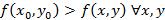
Данное соотношение определяет строгий максимум. При нестрогом знаке получается нестрогий максимум. Аналогично вводится локальный минимум.
Локальные максимумы и минимумы называются локальными экстремумами, если точка 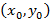– локальный экстремум для функции 
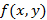, из которого следует, что 
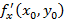и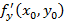 
равны нулю или не существуют. Обратное суждение неверно.
Пусть у функции 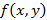существуют непрерывные частные производные до второго порядка включительно и 
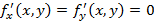, тогда существование экстремума зависит от выражения следующего вида
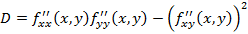
Если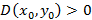 
, тогда экстремум есть, причем при 
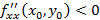– максимум и 
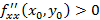– минимум. Если 
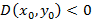, тогда экстремума в точке нет. Если 
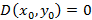, тогда нужны дополнительные исследования.
