Производная функции комплексной переменной

       Любая функция комплексной переменной может быть разделена на две части, которые являются функциями двух переменных. Для любой точки 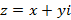 задается приращение  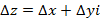– приращение аргумента, тогда приращение функции примет следующий вид 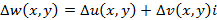, исходя из этого, производная функции комплексной переменной примет вид

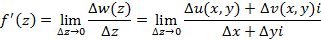
Полученное соотношение приращение аргумента стремится к нулю по любому пути от z до .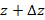

       Пусть в точке z функция 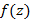 имеет производную 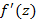, тогда исходя из определения получаем следующие соотношения

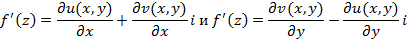
Из этого соотношения вытекают условия Коши-Римана

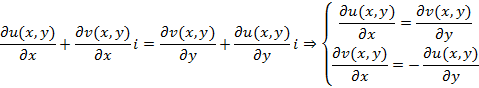
Условия Коши-Римана будут достаточными, если функция комплексной переменной будет иметь полный дифференциал, поскольку функции комплексной переменной всегда имеют полный дифференциал, тогда условия Коши-Римана являются необходимыми для существования производной функции комплексной переменной.

       Если функция 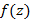 дифференцируема в окрестности точки z, тогда функция  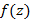является регулярной в точке z. Функция регулярна, поскольку она дифференцируема в любой точке на z-плоскости.

       Функци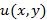и  и 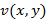, удовлетворяющие условиям Коши-Римана называются гармоническими. Гармонические функции удовлетворяют уравнениям Лапласа

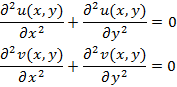
Гармонические функции называются сопряженными.