Несобственные интегралы первого и второго типа

       Пусть функция  непрерывна на луче 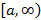, тогда для любого  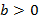существует интеграл вида 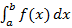, из этого следует, что можно рассмотреть соотношение, которое называется несобственным интегралом

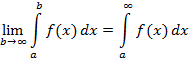
Если рассматриваемый предел существует и конечен, тогда интеграл называется сходящимся; если не существует или не конечен – расходящимся.

       Если 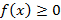 на луче 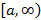, тогда геометрически несобственный интеграл считает площадь неограниченной фигуры, ограниченной прямой 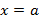. Пример подобной фигуры представлен на рисунке 51.

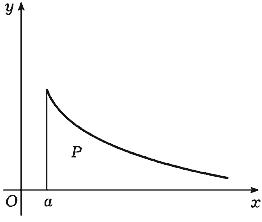
Рисунок 51. Фигура с площадью равной несобственному интегралу функции первого типа.

       Пусть функция  непрерывна на отрезке 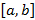 и существует вертикальная асимптота 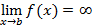, тогда для всех  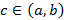заданная функция непрерывна. Исходя из этого, образуется несобственный интеграл второго типа, который определяется соотношением

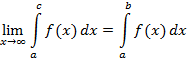
Если рассматриваемый приодел существует и конечен, тогда несобственный интеграл называется сходящимся, иначе расходящимся.

       Если 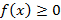 на отрезке 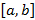, тогда несобственный интеграл считает площадь неограниченной фигуры, которая представлена на рисунке 52.

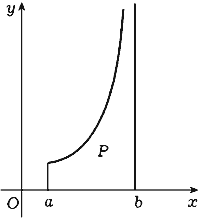
Рисунок 52. Фигура с площадью равной несобственному интегралу функции второго типа

       Несобственность интегралов первого и второго типа может быть как справа и слева, тогда получаемая фигура (рисунок 53) рассматривается на интервале 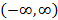 - бесконечный интервал.

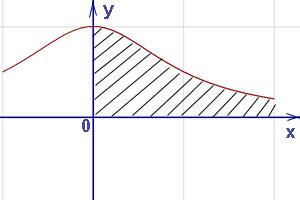
Рисунок 53. Фигура с площадью равной несобственному интегралу функции первого типа на бесконечном интервале.

Для несобственного интеграла второго типа возможен случай конечных пределов концов отрезов и разрыва функции  второго рода, пример представлен на рисунке 54.

Рисунок 54. Фигура с площадью равной несобственному интегралу функции второго типа, ограниченная функцией с разрывом второго рода.