Преобразования Лапласа – один из видов интегрального преобразования вида
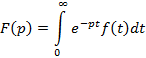
Где 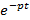 – ядро преобразования;
– ядро преобразования; 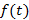 – функция оригинала;
– функция оригинала; 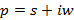 – комплексная переменная;
– комплексная переменная; 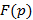 – изображение функции
– изображение функции 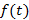
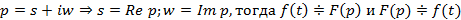
Функция оригинал 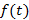 должна быть непрерывна за исключением конечного числа точек разрыва первого рода,
должна быть непрерывна за исключением конечного числа точек разрыва первого рода, 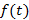 должна возрастать быстрее показательной функции и
должна возрастать быстрее показательной функции и 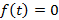 при
при 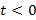 . Существует точка M и
. Существует точка M и 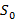 , такие что
, такие что 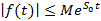 , где
, где 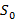 – показатель роста функции
– показатель роста функции 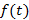 .
.
Для всякого оригинала 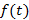 изображение
изображение 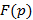 определено в полуплоскости
определено в полуплоскости
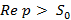 , где
, где 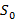 – показатель роста функции
– показатель роста функции 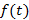 , и является в этой полуплоскости аналитической функцией
, и является в этой полуплоскости аналитической функцией
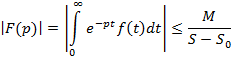
Исходя из этого утверждения следует, что
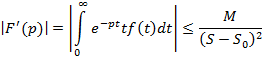
Из полученного соотношения следует справедливость следующего соотношения
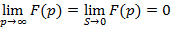
Примеры изображений для некоторых простейших функций
1. Единичная функция Хэвисайда
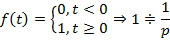
2. Линейная функция
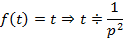
3. Степенная функция

4. Экспоненциальная функция, где, а – любое комплексное число
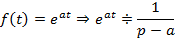
Теорема линейности: Если 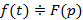 , а
, а 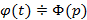 , тогда справедливо следующее
, тогда справедливо следующее
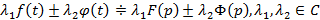
5. Тригонометрические функции
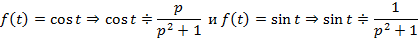
6. Гиперболические функции
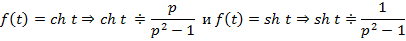
Теорема подобия: Если 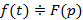 , тогда
, тогда 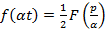 , где
, где 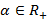 .
.
7. Тригонометрические функции с увеличением углов
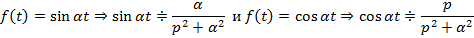
8. Гиперболические функции с увеличением углов
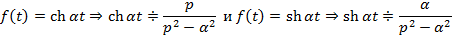
Терема дифференцирования оригинала: Если оригиналу 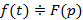 , тогда справедливо следующее
, тогда справедливо следующее 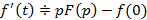 при условии, что
при условии, что 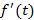 – оригинал. При непрерывности оригинала в точке
– оригинал. При непрерывности оригинала в точке 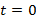 , тогда соотношение преобразуется следующим образом
, тогда соотношение преобразуется следующим образом
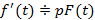 . Дифференцировать можно множество раз, тогда получим следующие соотношения
. Дифференцировать можно множество раз, тогда получим следующие соотношения
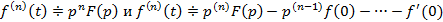
Теорема интегрирования оригинала: Если 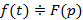 , тогда справедливо следующее соотношение
, тогда справедливо следующее соотношение
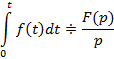
Теорема запаздывания: Если 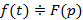 , тогда
, тогда 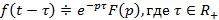 .
.
Теорема смещения: Если 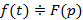 , тогда
, тогда 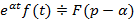 , где
, где 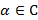 .
.
Теорема дифференцирования изображения: Если 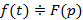 , тогда
, тогда 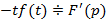
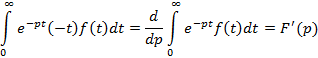
При производной n-го порядка получим
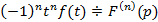
Теорема интегрирования изображения: Если 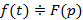 , тогда
, тогда
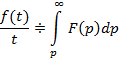
Теорема умножения: Если 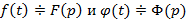 , тогда
, тогда 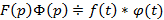 – свертка функций
– свертка функций 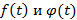
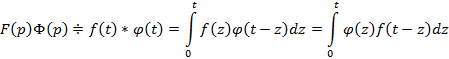
Теорема – интеграл Дюамеля: Если 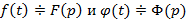 при
при 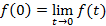 , тогда справедливо соотношение
, тогда справедливо соотношение
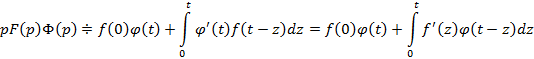
Теорема обращения: Преобразование вида 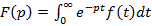 – прямое преобразование Лапласа, тогда соотношение следующего вида называется теоремой обращения
– прямое преобразование Лапласа, тогда соотношение следующего вида называется теоремой обращения
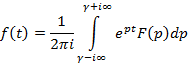
Данное соотношение справедливо для всех t, где 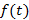 – непрерывна и
– непрерывна и 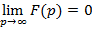 .
.
Следствие теоремы обращения – Правило Хэвисайда: Исходя из теоремы обращения справедливо следующее высказывание, устанавливающее связь оригинала и изображения
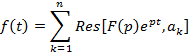
 2020-08-05
2020-08-05 130
130








