Тригонометрическим рядом называется ряд следующего вида, в котором 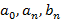 – коэффициенты ряда и период
– коэффициенты ряда и период 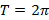

Пусть 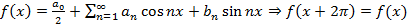 .
.
Пусть имеется сходящийся числовой ряд вида
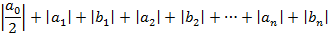
Исходя из этого тригонометрический ряд сходится равномерно, то позволяет почленно проинтегрировать этот ряд, в результате этого действия получим соотношения для коэффициентов
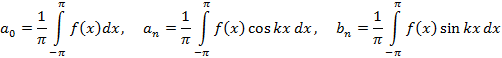
Функциональный ряд, который имеет вид тригонометрического ряда называется рядом Фурье, где 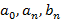 – коэффициенты ряда Фурье
– коэффициенты ряда Фурье
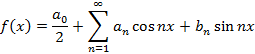
Если функция  периодическая с периодом
периодическая с периодом 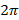 и непрерывна на интервале
и непрерывна на интервале 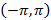 вместе со своей производной, за исключением конечного числа точек разрыва первого рода, тогда ряд Фурье для заданной функции сходится к этой функции во всех точках непрерывности функции, а в точках разрыва и на концах отрезка
вместе со своей производной, за исключением конечного числа точек разрыва первого рода, тогда ряд Фурье для заданной функции сходится к этой функции во всех точках непрерывности функции, а в точках разрыва и на концах отрезка 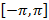 ряд сходится к среднему арифметическому ее предельных значений слева и справа.
ряд сходится к среднему арифметическому ее предельных значений слева и справа.
При произвольном периоде заданной функции разложение ряд Фурье производится с помощью замены переменной 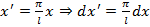 , что приводит к следующим соотношениям
, что приводит к следующим соотношениям
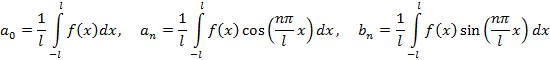
Дифференциальные уравнения
 2020-08-05
2020-08-05 103
103








