Дифференциальное решение первого порядка называется уравнение вида  , где
, где 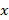 – независимая переменная,
– независимая переменная, 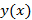 – неизвестная функция,
– неизвестная функция,  – производная неизвестной функции
– производная неизвестной функции 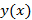 .
.
Если дифференциальное уравнение первого порядка можно записать в виде
 , тогда его называют разрешимым относительно производной. Функция
, тогда его называют разрешимым относительно производной. Функция
 называется решением дифференциального уравнения, если при подстановке она обращает его в верное тождество.
называется решением дифференциального уравнения, если при подстановке она обращает его в верное тождество.
У дифференциального уравнения бесконечно много решений. Чтобы выделить некоторое частное решение, необходимо задать пару чисел 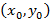 и требуется, чтобы график решения – интегральная кривая проходила через заданную точку. Пара чисел
и требуется, чтобы график решения – интегральная кривая проходила через заданную точку. Пара чисел 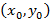 , где
, где 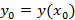 называется начальным условием для дифференциального уравнения. Задача нахождения решения дифференциального уравнения первого порядка с начальными условиями называется задачей Коши.
называется начальным условием для дифференциального уравнения. Задача нахождения решения дифференциального уравнения первого порядка с начальными условиями называется задачей Коши.
Теорема Коши: Если у дифференциального уравнения  правая часть является непрерывной как функция двух переменных вместе частной производной
правая часть является непрерывной как функция двух переменных вместе частной производной 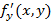 в некоторой области D, тогда начальное условие
в некоторой области D, тогда начальное условие 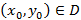 определяет единственное решение с заданными начальными условиями.
определяет единственное решение с заданными начальными условиями.
Общим решением дифференциального уравнения первого порядка, удовлетворяющего теореме Коши, называется семейство функций 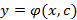 , такое что:
, такое что:
1. Для всех констант c функция 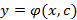 является решением;
является решением;
2. Для всех начальных условий 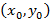 можно подобрать такое значение c, что
можно подобрать такое значение c, что
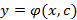 будет удовлетворять заданным начальным условиям.
будет удовлетворять заданным начальным условиям.
Решение дифференциального уравнения не всегда удается записать в явном виде.
Простейшие типы дифференциальных уравнений первого порядка:
1. Дифференциальное уравнение вида 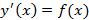 , общее решение которого имеет вид
, общее решение которого имеет вид
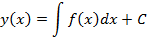
2. Уравнения с разделяющимися переменными – дифференциальные уравнения, в которых правая часть 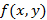 представлена как произведение
представлена как произведение 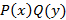 , иными словами, уравнение такого вида имеет вид
, иными словами, уравнение такого вида имеет вид
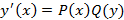
Алгоритм решения уравнения такого вида
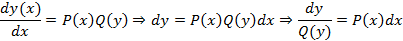
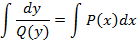
Полученное соотношение называется общим решением дифференциального уравнения. Если существует значение  , такое что
, такое что 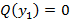 , тогда заданное значение также является решением дифференциального уравнения, но оно не входит в общее решение. Такое решение называется потерянным.
, тогда заданное значение также является решением дифференциального уравнения, но оно не входит в общее решение. Такое решение называется потерянным.
3. Если функция 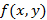 обладает свойством
обладает свойством 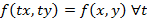 , тогда эта функция и дифференциальное уравнение называются однородными.
, тогда эта функция и дифференциальное уравнение называются однородными.
Однородные дифференциальные уравнения решаются с помощью замены переменной 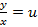 , где
, где 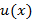 – новая неизвестная функция сведется к уравнению с разделяющимися переменными. В результате замены получим следующее соотношение
– новая неизвестная функция сведется к уравнению с разделяющимися переменными. В результате замены получим следующее соотношение
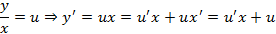
 2020-08-05
2020-08-05 112
112








