Пусть задана функция 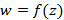 – аналитическая в некоторой области D, тогда ноли функции
– аналитическая в некоторой области D, тогда ноли функции 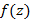 – точки
– точки  , в которой
, в которой  .
. 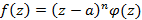 – ноль функции порядка n, при
– ноль функции порядка n, при 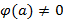 .
.
Устранимые особые точки (УОТ) – точки, в окрестности которых ряд Лорана не содержит главной части. Второй признак УОТ имеет вид
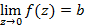
Существенно-особые точки (СОТ) – точки, в окрестности которых ряд Лорана содержит бесконечное число слагаемых в главной части.
Полюс – особая точка, в окрестности которой ряд Лорана содержит конечное число слагаемых в главной части. Если  – простой полюс. В полюсах и СОТ предел вида
– простой полюс. В полюсах и СОТ предел вида  бесконечен или не существует.
бесконечен или не существует.
Для того, чтобы изолированная особая точка a аналитической функции 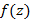 являлась полюсом m-го порядка, необходимо и достаточно, чтобы для функции вида
являлась полюсом m-го порядка, необходимо и достаточно, чтобы для функции вида 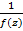 она являлась нулем m-го порядка.
она являлась нулем m-го порядка.
Вычеты аналитической функции комплексной переменной
Вычетом аналитической функции называется первый коэффициент главной части ряда Лорана функции 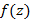 в особой точке a
в особой точке a

Вычисление вычета в полюсе m-го порядка примет вид
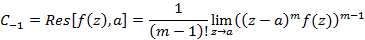
Исходя из этого вычет в полюсе второго порядка примет вид
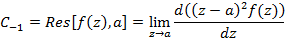
Вычет в простом полюсе примет вид
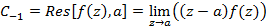
Если 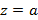 – простой полюс функции
– простой полюс функции 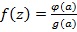 , где
, где 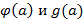 – аналитичны, тогда при
– аналитичны, тогда при  получим
получим
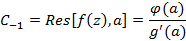
Теорема: Если функция 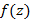 – аналитична в некоторой области D и непрерывна на контуре G за исключением конечного числа особых точек, тогда, на основании теоремы Коши для многосвязной области, справедливо следующее соотношение
– аналитична в некоторой области D и непрерывна на контуре G за исключением конечного числа особых точек, тогда, на основании теоремы Коши для многосвязной области, справедливо следующее соотношение
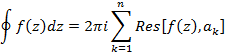
Вычисление интегралов в комплексной области
Пусть  , тогда при
, тогда при  и
и
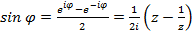 получим
получим
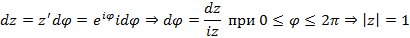
Из полученного соотношения получим вычисление интеграла функции 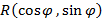
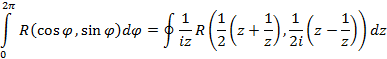
Если 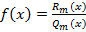 – рациональная функция непрерывная на Ox и
– рациональная функция непрерывная на Ox и 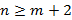 , тогда справедливо следующее соотношение для вычисления несобственного интеграла
, тогда справедливо следующее соотношение для вычисления несобственного интеграла
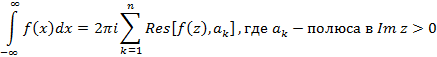
Если 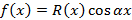 или
или 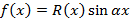 , где
, где  , тогда справедливо следующее соотношение
, тогда справедливо следующее соотношение
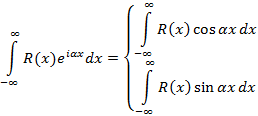
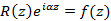 – аналитична в
– аналитична в  , тогда вычисление несобственного интеграла примет вид
, тогда вычисление несобственного интеграла примет вид

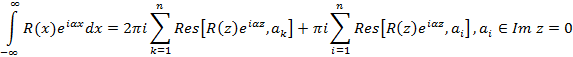
 2020-08-05
2020-08-05 187
187








