Степенной ряд, разложенный по степеням 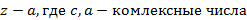 имеет вид
имеет вид
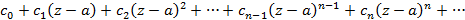
При 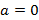 , получим
, получим 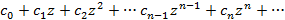 - степенной ряд, разложенный по степеням z.
- степенной ряд, разложенный по степеням z.
Теорема Абеля: Если степенной ряд комплексной переменной сходится при 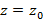 , тогда он сходится при любых z, удовлетворяющих условию
, тогда он сходится при любых z, удовлетворяющих условию 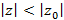 . Если заданный ряд расходится при
. Если заданный ряд расходится при 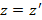 , тогда он расходится при
, тогда он расходится при  . Радиус сходимости
. Радиус сходимости 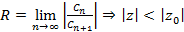 . Во всех точках внутри заданной окружности ряд сходится. Вне окружности – расходится. На границе окружности – нужны дополнительные исследования.
. Во всех точках внутри заданной окружности ряд сходится. Вне окружности – расходится. На границе окружности – нужны дополнительные исследования.
Степенной ряд, коэффициенты которого вычисляются функцией и ее производной, определяет ряд Тейлора в комплексной области
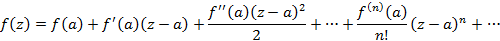
Теорема Тейлора: Пусть 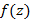 – аналитична в некоторой области D и непрерывная на контуре G, тогда в заданной области D функцию
– аналитична в некоторой области D и непрерывная на контуре G, тогда в заданной области D функцию 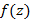 можно разложить в ряд Тейлора по интегральной формуле Коши
можно разложить в ряд Тейлора по интегральной формуле Коши
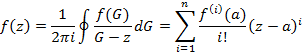
Частный случай ряда Тейлора – ряд Маклорена, который возникает при a в начале координат.
Ряд Лорана
Пусть задана некоторая точка a, ограниченная двумя окружностями таким образом, чтобы было справедливо соотношение 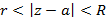 . Функция комплексной переменной
. Функция комплексной переменной 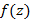 – аналитична и непрерывна в заданной кольцевой области.
– аналитична и непрерывна в заданной кольцевой области.
На основании интегральной теоремы Коши для многосвязной области получим соотношение

Исходя из этого соотношения получим ряд, состоящий из двух частей: правильная часть ряда Лорана – Тейлоровая и главная часть ряда Лорана – Лорановая
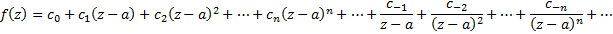
 2020-08-05
2020-08-05 175
175








