Если функция  дифференцируема в окрестности точки
дифференцируема в окрестности точки  бесконечное число раз, тогда степенной ряд следующего вида
бесконечное число раз, тогда степенной ряд следующего вида
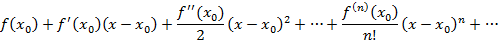
называется рядом Тейлора для функции  .
.
Достаточное условие представимости функции рядом Тейлора следующее: если в окрестности 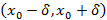 функция
функция  имеет производные, ограниченные по модулю одной общей константой
имеет производные, ограниченные по модулю одной общей константой 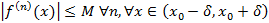 , иными словами ряд Тейлора в этой окрестности сходится к
, иными словами ряд Тейлора в этой окрестности сходится к  .
.
Ряд Тейлора при 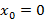 , иными словами
, иными словами
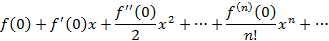
называется рядом Маклорена.
Разложение в ряд Маклорена некоторых функций
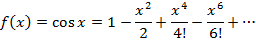
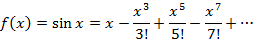
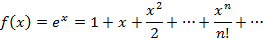
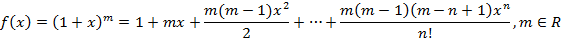
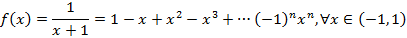
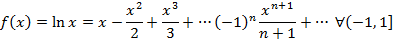
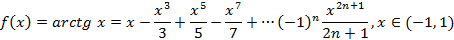
Основным практическим приложением рядом Маклорена является вычисление определенных интегралов с некоторой точностью, для чего подынтегральная функция раскладывается в ряд Маклорена и полученный ряд интегрируется почленно.
Ряды в комплексной области
Вся теория рядов в комплексной области сводится к поэлементному рассмотрению 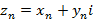 , из чего следует, что рассматриваются два ряда: действительный и мнимый, при этом, если расходится хотя бы один из них, тогда весь ряд расходится
, из чего следует, что рассматриваются два ряда: действительный и мнимый, при этом, если расходится хотя бы один из них, тогда весь ряд расходится
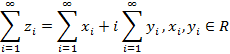
Функциональный ряд в комплексной области вида
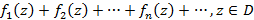
Сходится на области D, если в каждой точке заданной области ряд сходится. Если справедливо соотношение 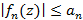 , тогда ряд сходится в области D равномерно – признак равномерной сходимости Вейерштрассе.
, тогда ряд сходится в области D равномерно – признак равномерной сходимости Вейерштрассе.
Если члены заданного ряда в комплексной области непрерывны в области D и заданный ряд равномерно сходится, тогда сумма ряда 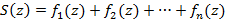 также непрерывна в области D. При тех же условиях справедливо также следующее соотношение
также непрерывна в области D. При тех же условиях справедливо также следующее соотношение
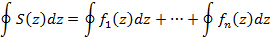
Если члены заданного ряда в комплексной области аналитичны в некоторой области D и ряд сходится в области D равномерно, тогда дифференциал суммы ряда примет вид
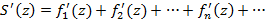
Ряд дифференциалов элементов ряда сводится к дифференциалу суммы ряда равномерно.
 2020-08-05
2020-08-05 135
135








