Дифференциальное уравнение вида 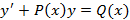 называется линейным дифференциальным уравнением первого порядка. Если
называется линейным дифференциальным уравнением первого порядка. Если 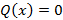 , тогда это линейное однородное дифференциальное уравнение
, тогда это линейное однородное дифференциальное уравнение 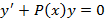 . Если
. Если 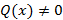 , тогда это линейное неоднородное дифференциальное уравнение.
, тогда это линейное неоднородное дифференциальное уравнение.
Линейное однородное дифференциальное уравнение – частный случай уравнения с разделяющимися переменными
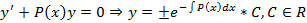
Полученное соотношение – общее решение линейного однородного дифференциального уравнения.
Теорема о структуре решений линейных неоднородных дифференциальных уравнений: Общее решение линейного неоднородного дифференциального уравнения всегда можно записать как сумму общего решения линейного однородного дифференциального уравнения  и любого частного решения заданного уравнения
и любого частного решения заданного уравнения 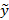
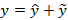
Теорема – Метод вариации постоянной: Если известно решение линейных однородных дифференциальных уравнений, тогда частное решение линейного неоднородного дифференциального уравнения всегда найдется в следующем виде
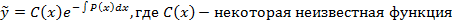
Уравнение Бернулли
Дифференциальное уравнение вида 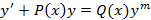 , где
, где  называется уравнением Бернулли. Уравнения данного вида легко преобразуются в линейные однородные и неоднородные дифференциальные уравнения.
называется уравнением Бернулли. Уравнения данного вида легко преобразуются в линейные однородные и неоднородные дифференциальные уравнения.
При решении уравнений Бернулли используется прием замены переменной, таким образом, чтобы оно преобразовалось в линейное неоднородное дифференциальное уравнение
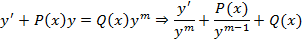
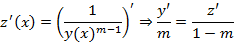
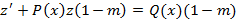
 2020-08-05
2020-08-05 102
102








