Пусть даны два множества 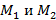 из
из 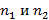 элементов соответственно. Число способов образовать пару таким образом, чтобы один элемент был из одного множества, а второй из второго, равно
элементов соответственно. Число способов образовать пару таким образом, чтобы один элемент был из одного множества, а второй из второго, равно  . Аналогично для трех элементов из множеств, число способов образовать тройку элементов равно
. Аналогично для трех элементов из множеств, число способов образовать тройку элементов равно  . Если имеется m множеств из
. Если имеется m множеств из 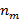 элементов, тогда существует
элементов, тогда существует 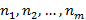 способов построить набор из m элементов.
способов построить набор из m элементов.
Пусть существует множество из n элементов и n упорядоченных ячеек. Каждое заполнение ячеек – перестановок равно соотношению

Есть множество из n элементов и m упорядоченных ячеек  . Каждое заполнение ячеек – размещение равно соотношению
. Каждое заполнение ячеек – размещение равно соотношению

Есть множество из n элементов и одна ячейка на m мест без упорядочивания. Каждое заполнение – сочетание равно соотношению

Геометрическая вероятность
Пусть 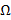 – некоторая область на прямой, плоскости или в пространстве; A – часть
– некоторая область на прямой, плоскости или в пространстве; A – часть 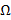 , тогда в опыте бросания точки в
, тогда в опыте бросания точки в 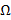 вероятность попадания в A равна соотношению
вероятность попадания в A равна соотношению

В данном соотношении мера – длина, площадь или объем. Рассматриваемое соотношение называется геометрической вероятностью.
У геометрической вероятности справедливы следующие свойства:
1. 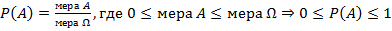 ;
;
2. Если A – невозможно, тогда A как множество пусто, тогда  ;
;
3. Если A – достоверное, тогда 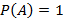 .
.
 2020-08-05
2020-08-05 95
95








