Равномерное распределение – непрерывная случайная величина X с функцией плотности распределения равной
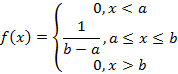
И функцией распределения соответственно равной
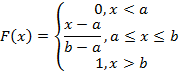
Графики функции плотности распределения и функции распределения равномерного распределения представлены на рисунке 58.
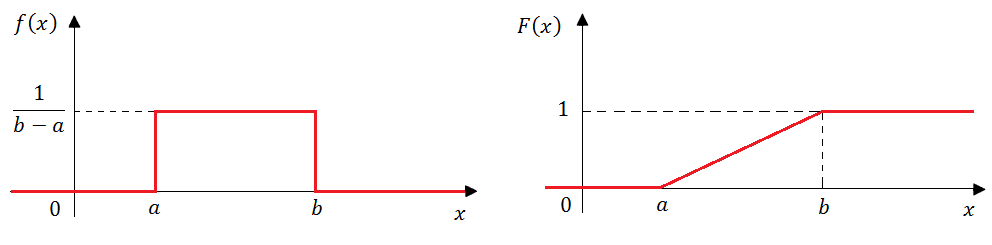
Рисунок 58. Графики функции плотности распределения и функции распределения равномерного распределения.
Математическое ожидание и дисперсия равномерно распределенной случайной величины соответственно равно
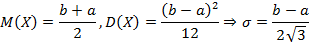
Равномерно распределённым являются те случайные величины, у которых значения заполняют отрезок 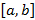 и равновозможные.
и равновозможные.
Нормальное распределение – распределение случайной величины с плотностью распределения равной
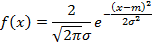
В данном соотношении 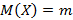 ,
, 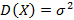 . Функция распределения нормального распределения имеет вид
. Функция распределения нормального распределения имеет вид
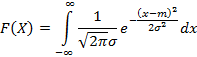
Данный интеграл не берущийся, поэтому функция распределения вычисляется приближенно. Функция распределения для стандартного случая нормального распределения 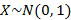 называется стандартной функцией распределения – функцией Лапласа
называется стандартной функцией распределения – функцией Лапласа
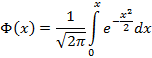
Применяя функцию Лапласа для нахождения вероятности нормально распределенной случайной величины получим соотношение
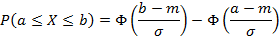
Теорема – Правило трех сигм: Для нормально распределённой случайной величины выход за пределы 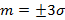 практически невозможно.
практически невозможно.
Графики плотности распределения и распределения нормально распределенной случайной величины представлено на рисунке 59.
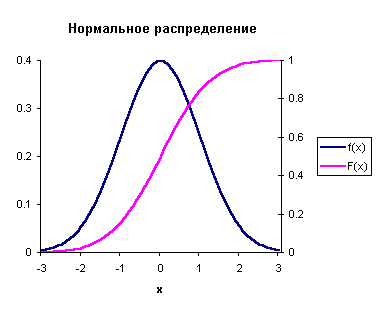
Рисунок 59. Графики функции плотности распределения и функции распределения нормального распределения.
Показательное распределение – распределение, которое задается функцией плотности распределения вида
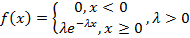
Функция распределения примет вид
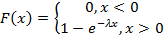
Графики функции плотности распределения и функции распределения представлены на рисунке 60.
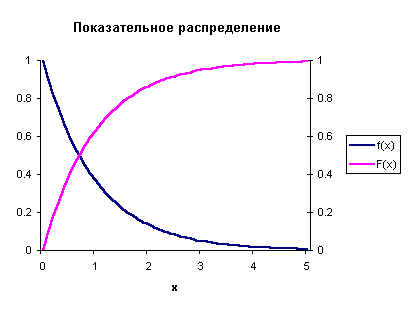
Рисунок 60. Графики функции плотности распределения и функции распределения показательного распределения.
Исходя из функции распределения получим соотношение для нахождения вероятности случайной величины
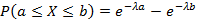
Математическое ожидание и дисперсия показательно распределенной случайной величины примет вид
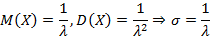
Закон больших чисел
Закон больших чисел – группа теорем, отражающих общий принцип, связанный с устойчивостью массовых случайных явлений. Конкретные особенности каждого случайного явления в массе взаимно поглощаются и почти не складываются на среднем результате.
Пусть даны  – независимые случайные величины с одинаковым законом распределения и, в частности, с одинаковым математическим ожиданием. Введем новую случайную величину
– независимые случайные величины с одинаковым законом распределения и, в частности, с одинаковым математическим ожиданием. Введем новую случайную величину
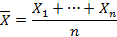
Исходя из этого, 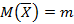 и
и 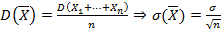 .
.
При большом числе опытов, рассматриваемая случайная величина не ведет себя как случайная величина, поскольку рассеивания практически нет.
Теорема Чебышева: Если 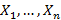 независимые и одинаково распределенные случайные величины с математическим ожиданием m, тогда справедливо следующее соотношение
независимые и одинаково распределенные случайные величины с математическим ожиданием m, тогда справедливо следующее соотношение
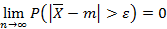
Центральная предельная теорема – группа теорем, связанных с законами распределения случайных величин, которые получаются при суммировании большого числа случайных величин.
Теорема Ляпунова: При суммировании большого числа независимых или слабо зависимых случайных величин закон распределения становится близким к нормальному, если каждое слагаемое слаб влияет на сумму.
При суммировании большого числа случайных величин математическое ожидание и дисперсия суммы могут неограниченно возрастать, поэтому рассматривают центрированную и нормированную сумму
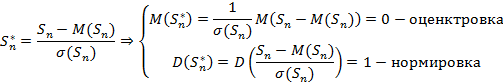
Теорема – предельная теорема Муавра-Лапласа: Пусть в схеме Бернулли каждый элемент принимает 0 – неудача или 1 – успех, тогда 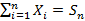 – число успехов в серии из n опытов. Исходя из этого, справедливо соотношение
– число успехов в серии из n опытов. Исходя из этого, справедливо соотношение
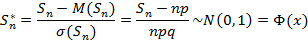
Вероятность суммы случайных величин примет вид
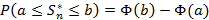
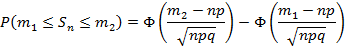
 2020-08-05
2020-08-05 183
183








