Пусть известно, что событие A имеет вероятность P. При проведении n опытов и фиксации количества наступления события A, тогда число 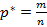 называют относительной частотой A в этих n опытов – статистический подход.
называют относительной частотой A в этих n опытов – статистический подход.
Исходя из теоремы Бернулли 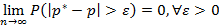 следует, что относительная частота
следует, что относительная частота 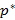 ведет себя устойчиво, иными словами, она колеблется около P и с увеличением числа опытов n эти колебания затухают. Исходя из этого, если P не известно, тогда берут
ведет себя устойчиво, иными словами, она колеблется около P и с увеличением числа опытов n эти колебания затухают. Исходя из этого, если P не известно, тогда берут 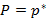 , при большом n – статистическая вероятность.
, при большом n – статистическая вероятность.
Пусть в серии из n независимых опытов нас интересует событие A в каждом опыте. Если оно произошло в конкретном опыте, тогда этот исход опыта – успешный и пусть p – вероятность успеха, соответственно 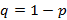 – вероятность неудачи. Исходя из всего выше сказанного, следует, что вероятность
– вероятность неудачи. Исходя из всего выше сказанного, следует, что вероятность 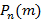 того, что в серии из n опытов ровно m успехов равно соотношению
того, что в серии из n опытов ровно m успехов равно соотношению
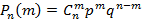
Данное соотношение – схема Бернулли.
При необходимости найти вероятность 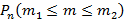 , тогда можно воспользоваться суммой несовместных событий
, тогда можно воспользоваться суммой несовместных событий
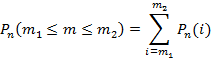
Свойства вероятности
Если A и B – совместные события, тогда 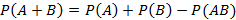 – теорема сложения вероятностей. При условии A и B – несовместные события, тогда справедливо следующее
– теорема сложения вероятностей. При условии A и B – несовместные события, тогда справедливо следующее 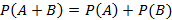 – следствие теоремы сложения вероятностей при
– следствие теоремы сложения вероятностей при 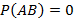 . Если
. Если 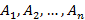 – попарно несовместные, тогда справедливо следующе соотношение
– попарно несовместные, тогда справедливо следующе соотношение
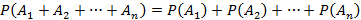
Если рассматриваемые n событий и в сумме они дают полную группу несовместных событий, тогда сумма их вероятностей равна единице.
Вероятностью A при условии B 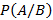 называется вероятностью события A при условии, что событие B точно произошло. Если событие B произошло, тогда пространство элементарных событий сужается до B при этом от A остается часть равная AB, тогда справедливо следующее соотношение, определяющее условную вероятность
называется вероятностью события A при условии, что событие B точно произошло. Если событие B произошло, тогда пространство элементарных событий сужается до B при этом от A остается часть равная AB, тогда справедливо следующее соотношение, определяющее условную вероятность
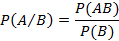
Событие A называется независимым от события B, если 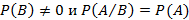 , иными словами, наступление или отсутствие события B не влияет на событие A.
, иными словами, наступление или отсутствие события B не влияет на событие A.
Пусть 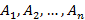 попарно несовместные события и в сумме дают все пространство несовместных событий, тогда эти события образуют полную группу несовместных событий, при этом вероятность любого случайного события B можно найти по формуле полной вероятности
попарно несовместные события и в сумме дают все пространство несовместных событий, тогда эти события образуют полную группу несовместных событий, при этом вероятность любого случайного события B можно найти по формуле полной вероятности
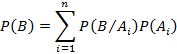
Данное соотношение определяется формулой Байеса
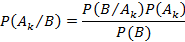
Случайные величины
Случайные величины – числовые величины, которые могут принимать в результате опыта то или иное значения, причем заранее не известно какое именно. Если все возможные значения случайной величины можно пронумеровать, тогда ее называют дискретной случайной величиной. Непрерывной случайной величиной называют случайные величины, которые занимают конечный или непрерывный промежуток целиком.
Любое правило, которое позволяет находить вероятность того, что случайная величина примет заданное значение или попадает в заданный промежуток значений называется законом распределения.
Пусть X принимает значения 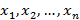 с вероятностями
с вероятностями 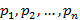 соответственно, тогда таблица типа значение-вероятность называется рядом распределения дискретной случайной величины. Графическое изображение данного ряда распределения – многоугольник распределения.
соответственно, тогда таблица типа значение-вероятность называется рядом распределения дискретной случайной величины. Графическое изображение данного ряда распределения – многоугольник распределения.
Случайная величина, которая принимает значения  с вероятностями равными
с вероятностями равными 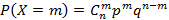 , где p – некоторое число из отрезка
, где p – некоторое число из отрезка 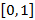 ;
; 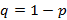 . Данные условия образуют ряд распределения вида
. Данные условия образуют ряд распределения вида 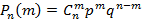 , который называется биноминальным распределением.
, который называется биноминальным распределением.
Если n в схеме Бернулли большое, тогда вычисления становятся очень громоздкими, поэтому при определении условных вероятностей можно воспользоваться приближенными формулами, такими как формула Пуассона
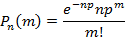
Для непрерывной случайной величины невозможно построить ряд распределения и вероятность принять конкретное значение равно нулю. Исходя из этого, целесообразно рассматривать вероятность вида 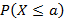 или
или 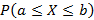 .
.
Функцией распределения случайной величины X называется функция следующего вида 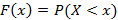 со свойствами:
со свойствами: 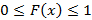 ,
, 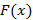 – не убывает,
– не убывает, 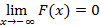 и
и 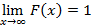 . Для любой непрерывной случайной величины справедливо следующие определения вероятности в случае нахождения значения на отрезке или на луче с известным началом
. Для любой непрерывной случайной величины справедливо следующие определения вероятности в случае нахождения значения на отрезке или на луче с известным началом
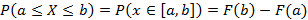
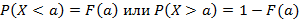
Сроить функцию распределения можно как для непрерывных случайных величин, так и для дискретных случайных величин В случае дискретного ряда распределения, функция распределения примет ступенчатый вид.
Если 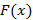 – функция распределения для непрерывной случайной величины, тогда ее производная
– функция распределения для непрерывной случайной величины, тогда ее производная 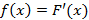 – функция плотности распределения непрерывной случайной величины.
– функция плотности распределения непрерывной случайной величины.
Свойства функции плотности распределения:
1. 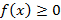 ;
;
2. 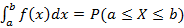 ;
;
3. 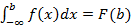 ;
;
4. 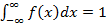 .
.
Исходя из указанных свойств, следует, что на всем интервале 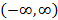 функция плотности распределения стремится к нулю.
функция плотности распределения стремится к нулю.
 2020-08-05
2020-08-05 108
108








