Выражение следующего вида называется квазимногочленом
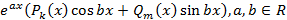
В данном выражении 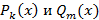 – многочлены степени k и m соответственно.
– многочлены степени k и m соответственно.
Пусть дано линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами и квазимногочленом, указанным выше, тогда найдется частное решение следующего вида
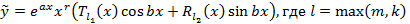
В данном соотношении 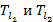 – многочлен степени
– многочлен степени 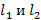 соответственно; r – кратность комплексного числа
соответственно; r – кратность комплексного числа 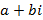 как корня характеристического уравнения, соответствующего линейному однородному дифференциальному уравнению. Если
как корня характеристического уравнения, соответствующего линейному однородному дифференциальному уравнению. Если 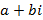 не корень, тогда
не корень, тогда
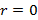 .
.
Многочлены 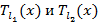 сначала записываются в общем виде с неопределенными коэффициентами, затем они просчитываются, подставив частное решение в линейное неоднородное дифференциальное уравнение.
сначала записываются в общем виде с неопределенными коэффициентами, затем они просчитываются, подставив частное решение в линейное неоднородное дифференциальное уравнение.
Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка следующего вида 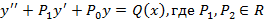 и
и 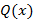 – произвольная правая часть, тогда общее решение можно записать в виде
– произвольная правая часть, тогда общее решение можно записать в виде
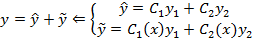
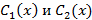 – некоторые функции, которые можно найти из системы следующего вида
– некоторые функции, которые можно найти из системы следующего вида
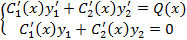
Решив данную систему, получим 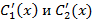 , а затем восстановим
, а затем восстановим 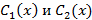 .
.
Теория вероятности и математическая статистика
 2020-08-05
2020-08-05 90
90








