Цель: сформировать умение решать задачи на нахождение количества элементов, используя правила комбинаторики
Теоретические сведения к практическому занятию:
Арккосинус числа 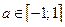 - это такое число
- это такое число 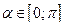 , косинус которого равен а, т.е.
, косинус которого равен а, т.е. 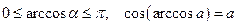 .
.
Если 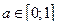 , то
, то 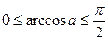 , а если
, а если 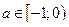 , то
, то 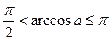 . Если
. Если 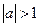 , то выражение
, то выражение  не имеет смысла.
не имеет смысла.
Для любого 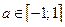 справедливо равенство
справедливо равенство 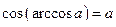 . Равенство
. Равенство 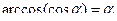 является верным только при
является верным только при 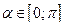 , хотя выражение
, хотя выражение  имеет смысл при всех
имеет смысл при всех 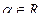 .
.
Для любого 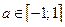 верно равенство
верно равенство 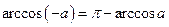 .
.
Арксинус числа 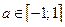 - это такое число
- это такое число 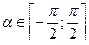 , синус которого равен а, т.е.
, синус которого равен а, т.е. 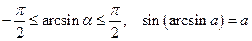 .
.
Если 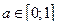 , то
, то 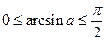 , а если
, а если 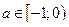 , то
, то 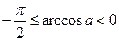 . Если
. Если 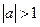 , то выражение
, то выражение 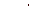 не имеет смысла.
не имеет смысла.
54
Для любого 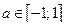 справедливо равенство
справедливо равенство 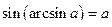 . Равенство
. Равенство 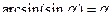 является верным только при
является верным только при 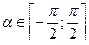 , хотя выражение
, хотя выражение 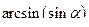 имеет смысл при всех
имеет смысл при всех 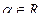 .
.
Для любого 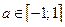 верно равенство
верно равенство 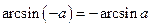 .
.
Для любого 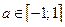 справедливо равенство
справедливо равенство 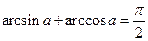 .
.
Арктангенс числа 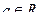 - это такое число
- это такое число 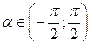 , тангенс которого равен а, т.е.
, тангенс которого равен а, т.е. 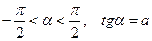 .
.
Для любого 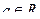 справедливо равенство
справедливо равенство 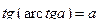 . Равенство
. Равенство 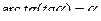 является верным только при
является верным только при 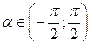 , хотя выражение
, хотя выражение 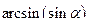 имеет смысл при всех
имеет смысл при всех 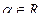 .
.
Для любого 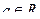 верно равенство
верно равенство 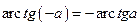 .
.
Пример: Вычислить 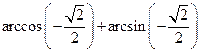
Решение:

Пример: Найти область определения функции 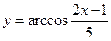
Решение:

Пример: Решить уравнение 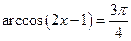
Решение:
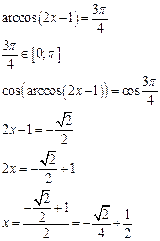
Самостоятельная работа:
1. Составьте кроссворд по теме «Основы тригонометрии» (от 8 до 15 слов)
Содержание практического занятия:
А. Ответить на вопросы:
1) Дайте определение арксинуса числа, укажите основные формулы для нахождения арксинуса числа. В каком случае выражение арксинуса числа не имеет смысл? Приведите примеры.
2) Дайте определение арккосинуса числа, укажите основные формулы для нахождения арккосинуса числа. В каком случае выражение арккосинуса числа не имеет смысл? Приведите примеры.
3) Дайте определение арктангенса числа, укажите основные формулы для нахождения арктангенса числа. Приведите примеры.
Б. Выполнить задания:
1. Вычислить:
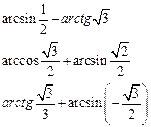
2. Найти область определения функции:
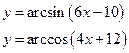
3.Найти область определения функции:
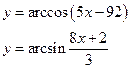
4. Решить уравнения:
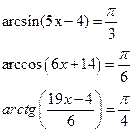
 2020-09-24
2020-09-24 92
92







