Цель: сформировать умение находить определители матриц.
Теоретические сведения к практическому занятию:
Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:
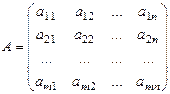 .
.
Вычисление определителей. Определитель матрицы A размера 2 x 2 (определитель 2-го порядка) – это число, которое можно найти по правилу:
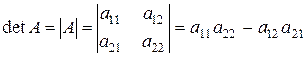
(произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали).
Определитель матрицы A размера 3 x 3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»:
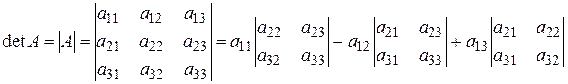
Пример 1. Найти: 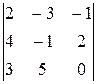
Решение. При нахождении определителя воспользуемся сначала формулой 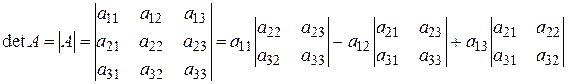 , а затем (для вычисления определителей 2-го порядка) формулой
, а затем (для вычисления определителей 2-го порядка) формулой 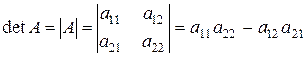 .
.
Самостоятельная работа:
Задание 1. Вычислить определители:
1) 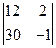
| 2) 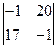 ; ;
| 3) 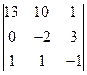
|
Содержание практического занятия:
А. Ответить на вопросы:
1) Дайте определение матрицы. Приведите примеры.
2) По какой формуле можно вычислить определитель матрицы размера 2х2?
3) По какой формуле можно вычислить определитель матрицы размера 3х3?
4) Приведите примеры нахождения определителей матриц различных размеров.
Б. Выполнить задания:
Задание 1. Вычислить определители:
1) 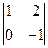
| 2) 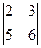
| 3) 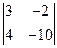
| 4) 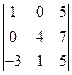
| 5) 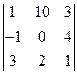
| 6) 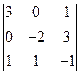
|
Тема: Системы линейных алгебраических уравнений: метод Крамера
Цель: сформировать умение решать системы алгебраических уравнений методом Крамера.
Теоретические сведения к практическому занятию:
Метод Крамера предназначен для того, чтобы решать системы линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равняется числу уравнений, а определитель основной матрицы не равен нулю.
Системами линейных алгебраических уравнений называют системы уравнений вида:
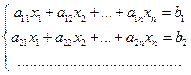
 2020-09-24
2020-09-24 102
102








