Цель: сформировать умение выполнять арифметические действия с комплексными числами.
Теоретические сведения к практическому занятию:
Комплексное число – это выражение вида
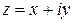 , (1.1)
, (1.1)
где x, y – вещественные числа, а  – мнимая единица. Первое из вещественных чисел, x, называется вещественной (действительной) частью комплексного числа (используется обозначение
– мнимая единица. Первое из вещественных чисел, x, называется вещественной (действительной) частью комплексного числа (используется обозначение 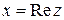 ); второе, y, - мнимой частью (
); второе, y, - мнимой частью (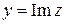 ). Выражение (1.1) называют алгебраической формой записи комплексного числа.
). Выражение (1.1) называют алгебраической формой записи комплексного числа.
Числом, сопряженным к 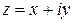 , называют число вида
, называют число вида  . Используя формулу разности квадратов, получаем, что
. Используя формулу разности квадратов, получаем, что 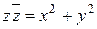 . Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.
. Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.
Пример 1. Решить уравнение 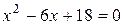 .
.
Решение. Дискриминант данного уравнения: 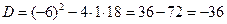 меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
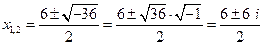 , т.е.
, т.е. 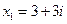 ;
; 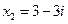 .
.
Справедливы следующие правила арифметических действий над комплексными числами  и
и 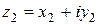 :
:
1) 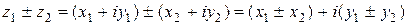 (осуществляется сложение или вычитание алгебраических двучленов и приведение подобных);
(осуществляется сложение или вычитание алгебраических двучленов и приведение подобных);
2) 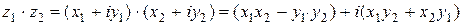 (осуществляется перемножение алгебраических двучленов и приведение подобных с учетом того, что
(осуществляется перемножение алгебраических двучленов и приведение подобных с учетом того, что 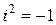 );
);
3) 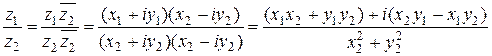 (эта операция возможна только в случае, когда
(эта операция возможна только в случае, когда 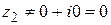 ).
).
Пример 2. Вычислить 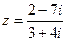 и указать вещественную и мнимую части полученного комплексного числа.
и указать вещественную и мнимую части полученного комплексного числа.
Решение. Действуя в соответствии с правилами получаем:
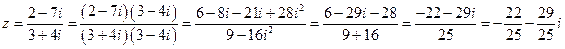 ;
;
поэтому 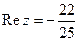 ,
, 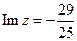 .
.
Тригонометрическая форма комплексного числа. Каждому комплексному числу вида (1.1) можно поставить в соответствие точку M(x;y) на декартовой плоскости (при этом на оси OX располагаются вещественные числа 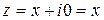 , а на оси OY – чисто мнимые числа
, а на оси OY – чисто мнимые числа 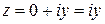 ).
).
Модулем комплексного числа назовем длину отрезка 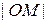 (или расстояние от начала координат до точки M), т.е.
(или расстояние от начала координат до точки M), т.е. 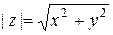 . Аргументом комплексного числа (
. Аргументом комплексного числа (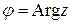 ) назовем угол, который вектор
) назовем угол, который вектор 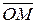 образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию
образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию 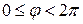 . При этом выражение вида
. При этом выражение вида
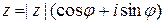 (1.2)
(1.2)
называется тригонометрической формой записи комплексного числа.
Преобразуем (1.1)
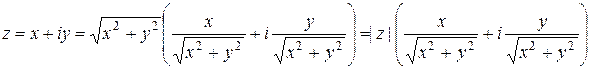
и, сравнивая с (1.2), получаем, что аргумент z можно найти, решив систему
 или
или 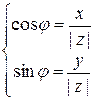 (1.3.)
(1.3.)
Пример 3. Записать комплексное число в тригонометрической форме 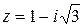 , указать модуль и аргумент комплексного числа.
, указать модуль и аргумент комплексного числа.
Решение. По определению 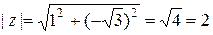 . Для определения аргумента воспользуемся формулой:
. Для определения аргумента воспользуемся формулой: 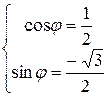 . Получаем, что
. Получаем, что 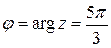 . Тригонометрическая форма заданного комплексного числа имеет вид:
. Тригонометрическая форма заданного комплексного числа имеет вид:  .
.
Возведение в степень и извлечение корней. Если комплексное число задано тригонометрической формой 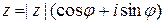 , то справедлива формула Муавра
, то справедлива формула Муавра
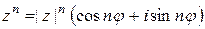 . (1.4)
. (1.4)
Для извлечения корня n -й степени (n – целое число, большее 1) из комплексного числа, заданного в тригонометрической форме, применяется формула, дающая n значений этого корня:
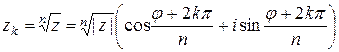 , k=0,1,…,n-1. (1.5)
, k=0,1,…,n-1. (1.5)
Самостоятельная работа:
Задание 1. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
1) 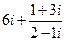 2)
2) 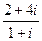 3)
3) 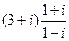 4)
4) 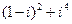
Задание 2. Найти все корни уравнений:
1)  ; 2)
; 2)  ; 4)
; 4) 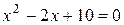 ;
;
5) 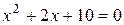 ; 6)
; 6) 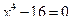 7)
7) 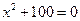
Содержание практического занятия:
А. Ответить на вопросы:
1) Дайте определение комплексного числа. Приведите примеры.
2) Как называется каждая из частей комплексного числа? Приведите примеры.
3) Какое число называется числом, сопряженным к комплексному числу? Приведите примеры.
4) Назовите основные арифметические действия над комплексными числами. Приведите примеры.
Б. Выполнить задания:
Задание 1. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
1) 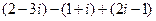 2)
2)  3)
3) 
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
1) 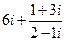 2)
2) 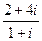 3)
3) 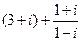 4)
4) 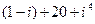
 2020-09-24
2020-09-24 176
176








