Практическое занятие №3

Наименование занятия: Решение уравнений методом итераций

Цель занятия: Научиться решать уравнения методом простой итерации, использовать программные средства для проверки правильности найденного результата. Формировать ОК-2,  ОК-3, ОК-5, ОК-6, ОК-7, ОК-9, овладеть знаниями и умениями, необходимыми для освоения ПК- 1.2.

Подготовка к занятию: Повторить теоретический материал по теме «Приближенные методы решения уравнений»: метод итераций.

Литература:

1. Лобачева М.Е. Численные методы. Учебное пособие, 2015г.

Перечень необходимых приборов, инструментов, материалов: ПЭВМ

Задание на занятие:

1. Отделить графически корни данного уравнения.
2. Уточнить корни методом простой итерации с точностью до

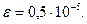
Варианты заданий:

№ варианта	Уравнение
1
2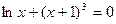
3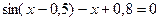
4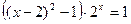
5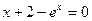
6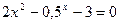
7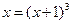
8
9
10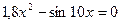

Порядок проведения занятия:

1. Получить допуск к работе.

2. Отделить графически отрезок [ a;b ] небольшой длины h, изолирующий один из корней уравнения f(x) = 0.

3. Привести исходное уравнение к виду x=g(x), пригодному для метода простой итерации на отрезке [ c;d ] = [ a-h;b+h ].

4. Составить программу вычисления приближений до достижения требуемой точности .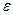

5. Найти приближенный корень уравнения и выписать его с верными значащими цифрами.

6. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель работы, задание;

2. Выполненное задание (отделенные графически корни уравнения, результаты, полученные методом простой итерации);

3. Выводы по результатам выполненного задания;

4. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Какими способами можно привести уравнение f(x)= 0 к равносильному уравнению x=g(x) с требуемыми для метода свойствами?

2. Какие условия гарантируют сходимость итерационной последовательности к корню уравнения?

3. Какова последовательность действий при решении уравнений методом простой итерации?

4. Какое условие является критерием достижения заданной точности при решении уравнения методом простой итерации?

ПРИЛОЖЕНИЕ