Теорема 1. Дифференциал суммы двух дифференцируемых функций 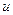 и
и 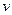 равен сумме дифференциалов этих функций:
равен сумме дифференциалов этих функций:
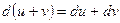 .
.
Теорема 2. Дифференциал произведения двух дифференцируемых функций 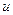 и
и 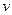 определяется по формуле:
определяется по формуле:
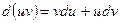 .
.
Теорема 3. Дифференциал частного двух дифференцируемых функций 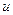 и
и 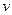 определяется по формуле:
определяется по формуле:
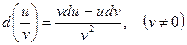 .
.
Производные различных порядков
Пусть на некотором множестве 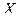 определена дифференцируемая функция
определена дифференцируемая функция 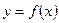 . Производная
. Производная 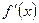 этой функции также является функцией от
этой функции также является функцией от 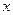 . Следовательно, можно говорить о производной этой функции, т.е. о производной от первой производной. Если она существует, то её называют производной второго порядка функции
. Следовательно, можно говорить о производной этой функции, т.е. о производной от первой производной. Если она существует, то её называют производной второго порядка функции 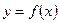 или второй производной от первоначальной функции и обозначают
или второй производной от первоначальной функции и обозначают  или
или 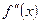 :
:
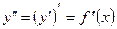 .
.
Аналогично, если существует производная от второй производной, то она называется производной третьего порядка или третьей производной и обозначается через 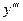 или
или 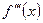 :
:
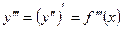 .
.
Производной n-го порядка от функции  называется производная первого порядка от производной
называется производная первого порядка от производной 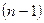 -го порядка и обозначается символом
-го порядка и обозначается символом 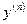 или
или 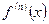 :
:
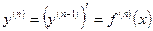 .
.
Производные четвёртого, пятого и высших порядков обозначаются 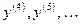 или
или 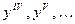 .
.
Примеры:
1) Найдите 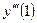 для функции
для функции  .
.
Решение. 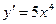 ,
, 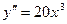 ,
, 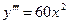 ,
, 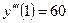 .
.
2) Найдите 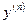 для функции
для функции 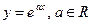 .
.
Решение. 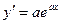 ,
, 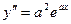 ,
, 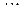 ,
, 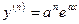 .
.
Докажем формулу для 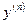 методом математической индукции.
методом математической индукции.
Для 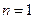 получаем
получаем 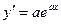 , таким образом, формула верна.
, таким образом, формула верна.
Предположим, что формула верна для 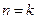 , т.е.
, т.е. 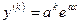 .
.
Докажем, что формула верна для 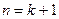 :
:
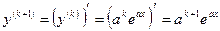 .
.
Таким образом, формула верна для любого 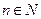 .
.
Для производных n-го порядка справедливы формулы:
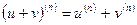 ,
,
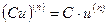 ,
,
а также формула Лейбница:
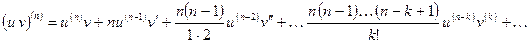
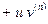 .
.
Тема 8. ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
Теорема о корнях производной (теорема Ролля)
Теорема Ролля. Если функция 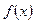 :
:
1) непрерывна на отрезке 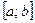 ;
;
2) дифференцируема на интервале 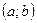 ;
;
3) 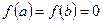 ;
;
то существует, по крайней мере, одна точка 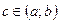 , для которой
, для которой 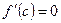 .
.
 2020-09-24
2020-09-24 185
185








