Теорема 1. Если функции 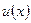 и
и 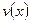 дифференцируемы на некотором интервале, то на этом интервале
дифференцируемы на некотором интервале, то на этом интервале
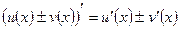
т.е. производная суммы (разности) функций равна сумме (разности) производных этих функций.
Теорема 2. Если функции 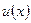 и
и 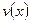 дифференцируемы на некотором интервале, то на этом интервале
дифференцируемы на некотором интервале, то на этом интервале
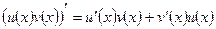 .
.
Следствие. Постоянный множитель можно выносить за знак производной, т.е. 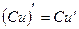 , где
, где 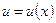 - дифференцируемая функция.
- дифференцируемая функция.
Теорема 3. Если функции 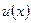 и
и 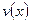 дифференцируемы на некотором интервале и
дифференцируемы на некотором интервале и 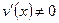 для любого x из этого интервала, то
для любого x из этого интервала, то
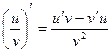 .
.
Производные некоторых элементарных функций
1. 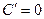 9.
9. 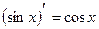
2. 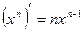 10.
10. 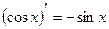
3. 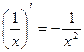 11.
11. 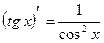
4. 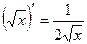 12.
12. 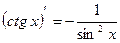
5. 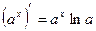 13.
13. 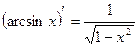
6. 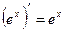 14.
14. 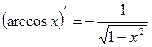
7. 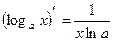 15.
15. 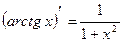
8. 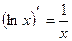 16.
16. 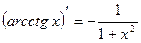
Пример: Найдите производную функции 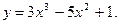
Решение. По теореме 1 и следствию из теоремы 2 получаем:
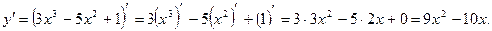
Пример: Найдите производную функции 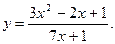
Решение. По теореме 3 получаем:
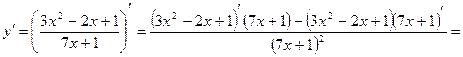
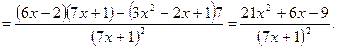
Производная сложной функции
Пусть задана сложная функция 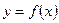 , т.е. такая, что её можно представить в виде:
, т.е. такая, что её можно представить в виде:
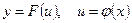
или 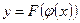 . В выражении
. В выражении 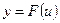 переменная u называется промежуточным аргументом.
переменная u называется промежуточным аргументом.
Теорема. Если функция 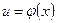 имеет в некоторой точке x производную
имеет в некоторой точке x производную 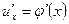 , а функция
, а функция 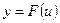 имеет при соответствующем значении u производную
имеет при соответствующем значении u производную 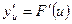 , то сложная функция
, то сложная функция 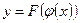 в указанной точке x также имеет производную, которая равна
в указанной точке x также имеет производную, которая равна
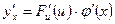 ,
,
где вместо u должно быть подставлено выражение 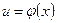 .
.
Коротко,
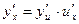 ,
,
т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.
Пример: Дана функция 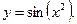 . Найдите
. Найдите 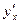 .
.
Решение. Введем промежуточный аргумент u:
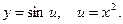
Тогда 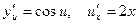 . По правилу дифференцирования сложной функции получаем:
. По правилу дифференцирования сложной функции получаем:
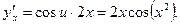
Следствие. Если функция 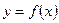 такова, что её можно представить в виде
такова, что её можно представить в виде 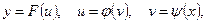 то
то

Пример: Дана функция 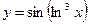 . Найдите
. Найдите 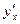 .
.
Решение. Пусть 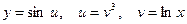 . Тогда
. Тогда 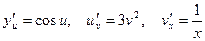 . По рассмотренному выше следствию получаем:
. По рассмотренному выше следствию получаем:
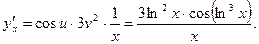
 2020-09-24
2020-09-24 200
200








