Геометрический смысл производной

Пусть - дуга некоторой линии и – точка этой линии, 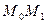- секущая. Если точка 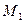приближается по дуге к точке , то секущая 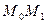будет поворачиваться вокруг точки и стремиться к некоторому предельному положению . Тогда прямая 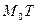называется касательной к линии в точке .

Определение. Касательной к линии в точке называется прямая, к которой стремится секущая 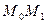, когда стремится к .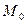

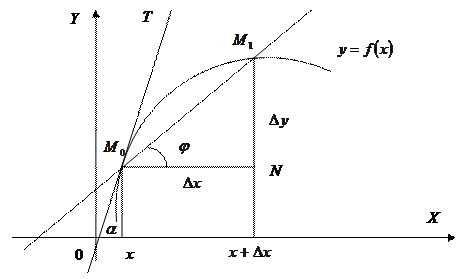
Рассмотрим функцию 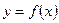. Возьмём на графике функции точк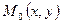и и .

Из прямоугольного треугольника получаем , тогда

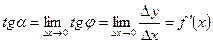Следовательно, значение производной в данной точке x равняется тангенсу угла, образованному касательной к графику функции 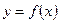в соответствующей точке с положительным направлением оси Ox.

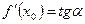
Пример: Найдите тангенсы углов наклона касательной к кривой в точках , .

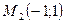Решение. , .

Механический смысл производной

Если при прямолинейном движении точки задан закон движения , то скорость движения в момент есть производная пути по времени:

Пример: Материальная точка движется прямолинейно по закону 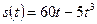. Через сколько времени после начала движения точка остановится? Найдите путь, пройденный точкой до остановки.

Решение. В момент остановки скорость точки равна нулю. Находим . Решаем уравнение , т.е. 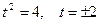. Таким образом, после начала движения точка остановится через 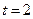с. Путь, пройденный точкой до остановки, составит м.